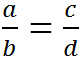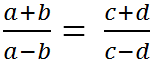Giải bài 63 trang 31 - Sách giáo khoa Toán 7 tập 1

Đề bài

 Chứng minh tỉ lệ thức

(a - b ≠ 0, c - d ≠ 0) ta có thể suy ra tỉ lệ thức

Hướng dẫn giải

Đặt \(\dfrac{a}{b} = \dfrac{c}{d} =k\)

Vì a - b \(\neq\) 0 , c - d \(\neq\) 0 nên a \(\neq\) b , c \(\neq\) d, do đó :

a = bk, c = dk

\(\dfrac{a+b}{a-b}=\dfrac{bk+b}{bk-b}= \dfrac{b(k+1)}{b(k-1)}=\dfrac{k+1}{k-1}\)           (1)

\(\dfrac{c+d}{c-d}=\dfrac{dk+d}{dk-d}= \dfrac{d(k+1)}{d(k-1)}=\dfrac{k+1}{k-1}\)           (2)

Từ (1) và (2) suy ra :

\(\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)