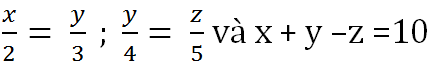Giải bài 61 trang 31 - Sách giáo khoa Toán 7 tập 1
Đề bài
Hướng dẫn giải
BCNN(3;4) = 12 nên ta biến đổi như sau :
\(\dfrac{x}{2}=\dfrac{y}{3} \Rightarrow \dfrac{x}{2.4} = \dfrac{y}{3.4} \Rightarrow \dfrac{x}{8}= \dfrac{y}{12}\) (1)
\(\dfrac{y}{4}=\dfrac{z}{5} \Rightarrow \dfrac{y}{3.4} = \dfrac{z}{5.3} \Rightarrow \dfrac{y}{12}= \dfrac{z}{15}\) (2)
Từ (1) và (2) suy ra \(\dfrac{x}{8} = \dfrac{y}{12}=\dfrac{z}{15}\)
Theo tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{8} = \dfrac{y}{12}=\dfrac{z}{15} = \dfrac{x+y-z}{8+12-15} = \dfrac{10}{5}=2\)
\(\Rightarrow\) x = 8.2 = 16
y = 12.2 = 24
z = 15.2 = 30
Vậy x = 16 ; y = 24; z = 30