Giải bài 38 trang 62 - Sách giáo khoa Toán 9 tập 1
Đề bài
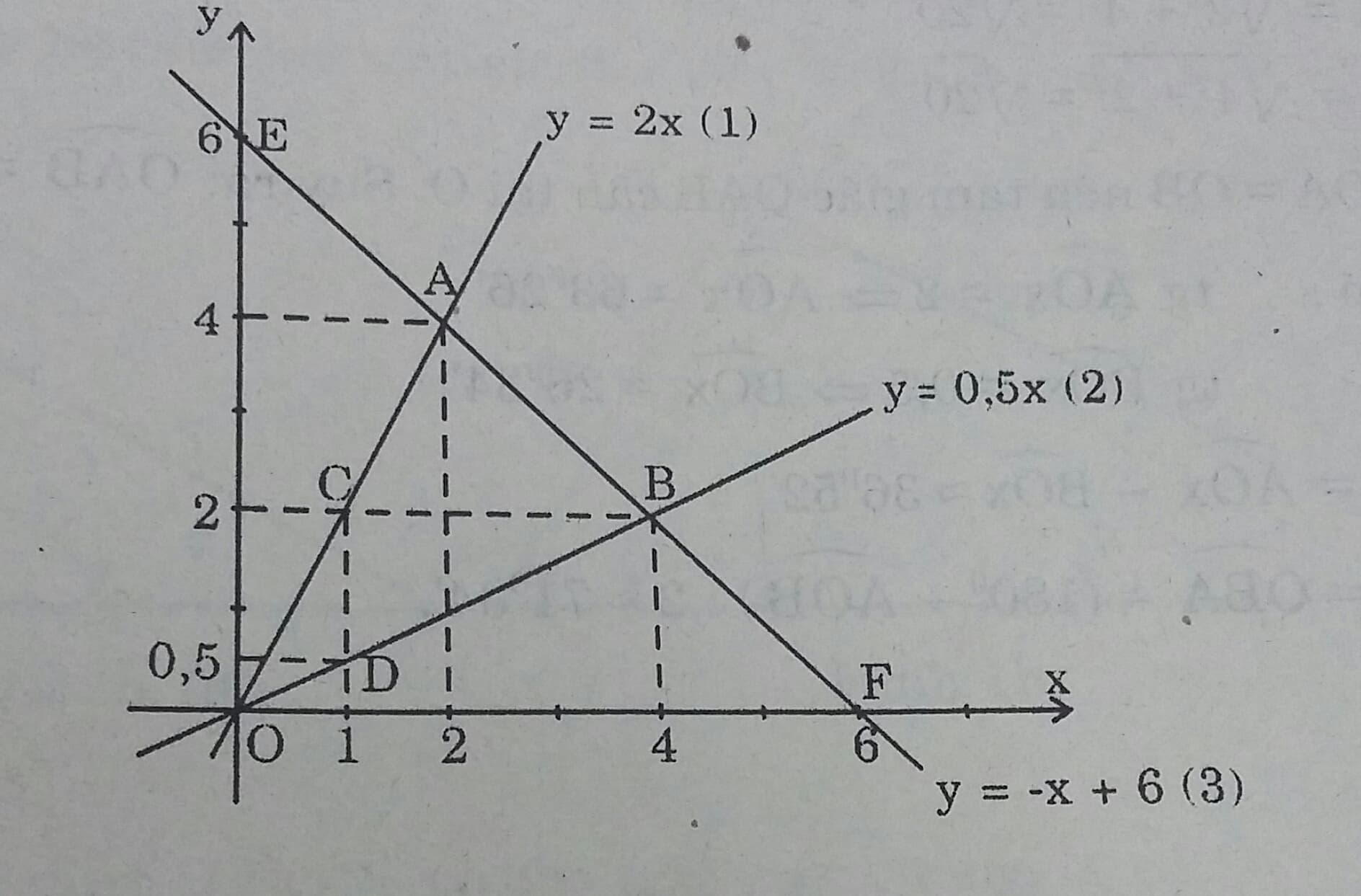
a) Vẽ đồ thị các hàm số sau trên cùng một mặt phẳng tọa độ:
y = 2x (1); y = 0,5x (2); y = -x + 6 (3)
b) Gọi các giao điểm của đường thẳng có phương trình (3) với hai đường thẳng có phương trình (1) và (2) theo thứ tự là A và B. Tìm tọa độ của hai điểm A và B.
c) Tính các góc của tam giác OAB.
Hướng dẫn câu c)
Tính OA, OB rồi chứng tỏ tam giác OAB là tam giác cân.
Hướng dẫn giải
Hướng dẫn:
Tính các góc tam giác OAB:
- Tính OA, Ob từ đó suy ra tam giác OAb cân tại O để được \( \widehat{ OAB}=\widehat{ OBA}\)
- Tính \(\widehat{ AOB }=\widehat{ AOx }-\widehat{ BOx}\)
- Tính \(\widehat{ OAB }=\widehat{ OBA}=(180^0-\widehat{ AOB }):2 \)
Giải:
a) Đường thẳng y=2x đi qua gốc tọa độ O(0;0) và điểm C(1;2)
Đường thẳng y=0,5x đi qua gốc tọa độ O(0;0) và điểm \(D(1; \frac{2}{3})\)
Đường thẳng y =-x+6 đi qua hai điểm E(0;6) và F(6;0).
b) Hoành độ giao điểm A là nghiệm của phương trình hoành độ:
2x= -x+6 \(\Leftrightarrow x=2 \)
Thay x=2 vào hàm số y=2x được y=4. Vậy: A(2;4)
Hoành độ giao điểm B là nghiệm của phương trình hoành độ:
0,5x=-x+6 \(\Leftrightarrow x=4 \)
Thay x=4 vào hàm số y=0,5x được y=2. Vậy B(4;2)
c) Áp dụng định lý Py-ta-go cho các tam giác vuông, ta có:
\(OA= \sqrt{2^2+4^2}=\sqrt{20}\)
\(OB= \sqrt{2^2+4^2}=\sqrt{20}\)
Do OA=OB nên tam giác OAB cân tại O.Suy ra: \( \sqrt{OAB}=\sqrt{OBA}\)
Ta có: \(tg \widehat{ AOx }=2 \Rightarrow \widehat{ AOx} \approx 63^026'\)
\(tg \widehat{ BOx }=0,5 \Rightarrow \widehat{ BOx} \approx 26^034'\)
\( \widehat{ OAB }=\widehat{ A0x}-\widehat{ BOx} \approx 36^026'\)
\( \widehat{OAB } = \widehat{OBA } \approx (180^0 - \widehat{ AOB}) : 2 \approx 71^034'\)

