Giải bài 28 trang 80 - Sách giáo khoa Toán 8 tập 1
Đề bài
Cho hình thang ABCD (AB // CD), E là trung điểm của AD, F là trung điểm của BC. Đường thẳng EF cắt trung điểm của AD, F là trung điểm của BC. Đường thẳng EF cắt BD tại I, cắt AC ở K.
a) Chứng minh rằng AK = KC, BI = ID.
b) Cho AB = 6cm, CD = 10cm. Tính các độ dài EI, KF, IK.
Hướng dẫn giải
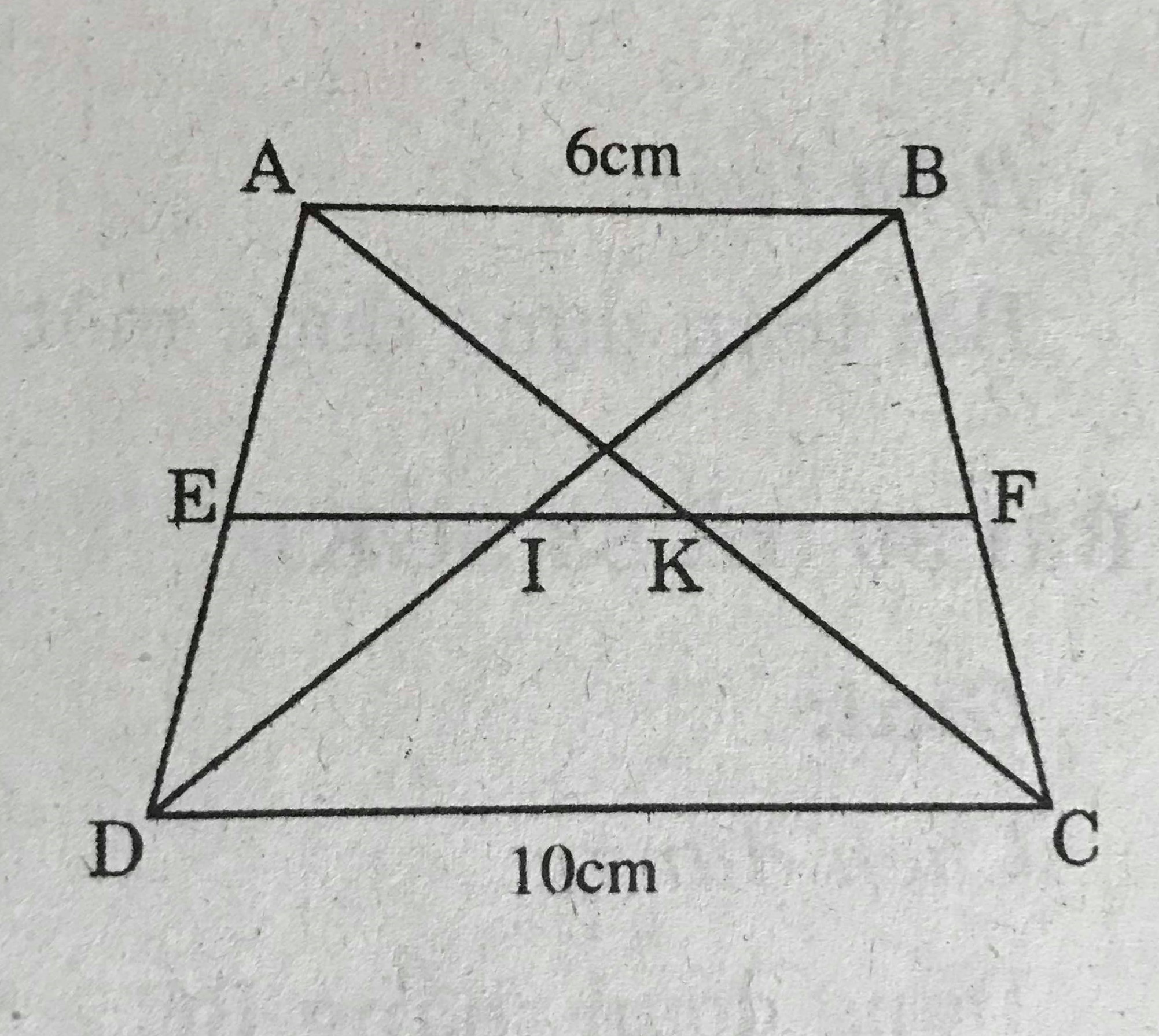
a) Xét tứ giác ABCD , ta có :
FB = FC (gt); EA = ED (gt)
Vậy, EF là đường trung bình của hình thang ABCD nên EF // AB // CD.
ΔABC có BF = FC và FK // AB nên AK = KC.
ΔABD có AE = ED và EI // AB nên BI = ID.
b) Vì EF là đường trung bình của hình thang ABCD theo a nên:
EF = \(\dfrac{AB+CD}{2}\) = \(\dfrac{6+10}{2}\) = 8 (cm)
Xét ΔDAB , ta có : EA = ED ; ID = IB
Vậy, EI là đường trung bình của ΔDAB .
EI = \(\dfrac{AB}{2}=\dfrac{6}{2}=3\) (cm); KF = \(\dfrac{AB}{2}=3\) (cm)
IK = EF - EI - KF = 8 - 3 - 3 = 2 (cm)

