Giải bài 27 trang 80 - Sách giáo khoa Toán 8 tập 1

Đề bài

Cho tứ giác ABCD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, AC.

a) So sánh các độ dài EK và CD, KF và AB

b) Chứng minh rằng

EF \(\leq\) \(\dfrac{AB+CD}{2}\)

 

Hướng dẫn giải

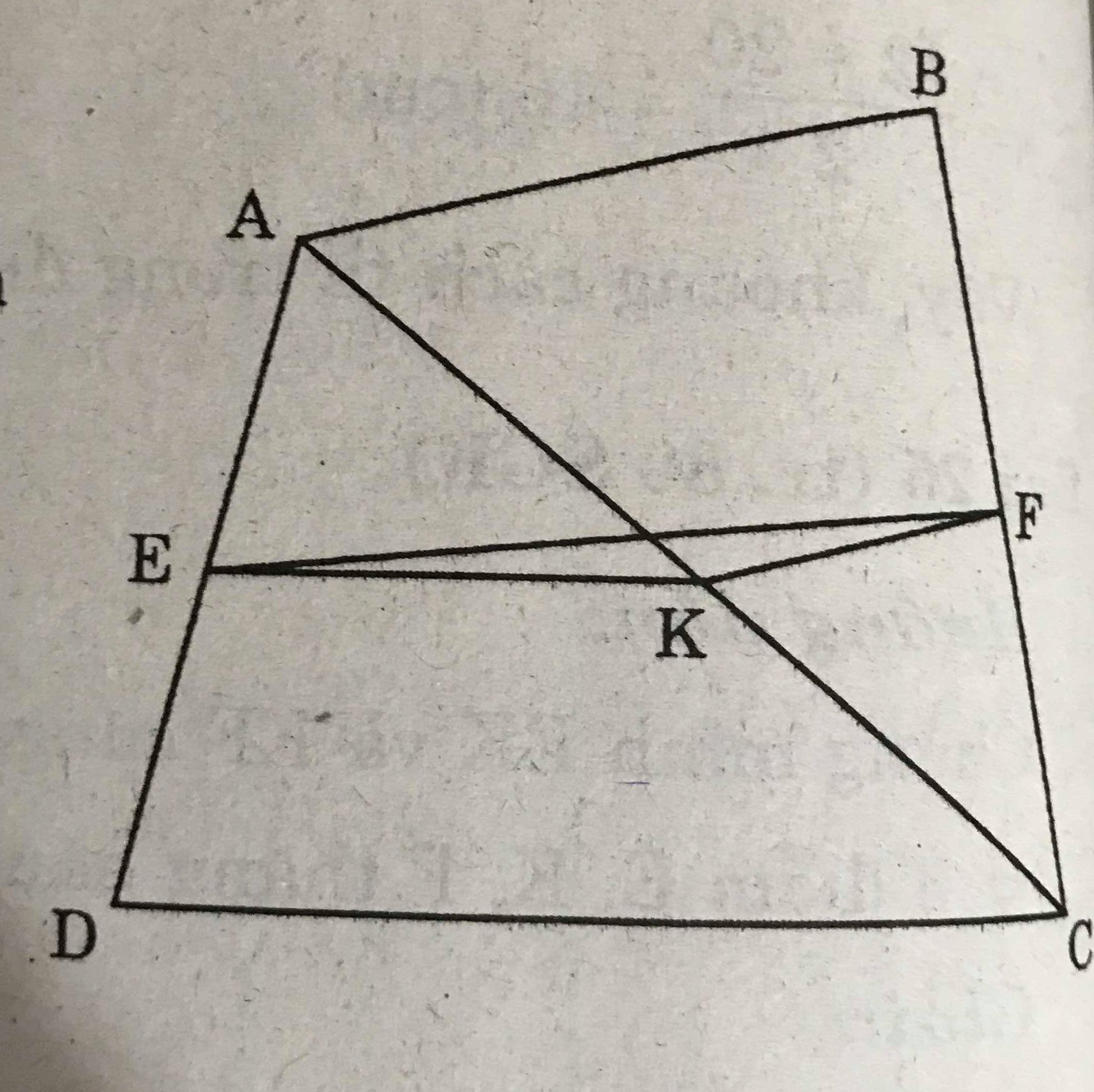
a) Theo giả thiết , ta có :

EA = ED ; KA = KC

Vậy, EK là đường trung bình của tam giác ADC.

=> EK = \(\dfrac{CD}{2}\)

Tương tự KF là đường trung bình của tam giác ABC.

=> KF = \(\dfrac{AB}{2}\)

b) Áp dụng tính chất bất đẳng thức trong tam giác EFK , ta có :

EF \(\leq\) EK + KF = \(\dfrac{CD}{2}\)+\(\dfrac{AB}{2}\)= \(\dfrac{AB+CD}{2}\)