Giải bài 25 trang 55 - Sách giáo khoa Toán 9 tập 1

Đề bài

   a) Vẽ đồ thị của hàm số sau trên cùng một mặt phẳng tọa độ:

   b, Một đường thẳng song song với trục hoành Ox, cắt trục tung Oy tại điểm có tung độ bằng 1, cắt các đường thẳng

theo thứ tự tại hai điểm M và N. Tìm tọa độ của hai điểm M và N.

Hướng dẫn giải

    Hướng dẫn: 

- Đường thẳng song song với trục hoành Ox và cắt trục tung tại điểm có tung độ bằng b và có dạng y=b.

- Hoành độ giao điểm của hai đường thẳng y=ax+b và y=a'x +b' là nghiệm của phương trình: ax+b = a'x+b'

   Giải: 

   a) Đồ thị hàm số \(y= \frac{2}{3}x+2 \) đi qua hai điểm ( 0;2) và ( -3; 0).

   Đồ thị hàm số \(y=- \frac{2}{3}x+2 \) đi qua hai điểm (0;2) và \((\frac{4}{3};0)\) 

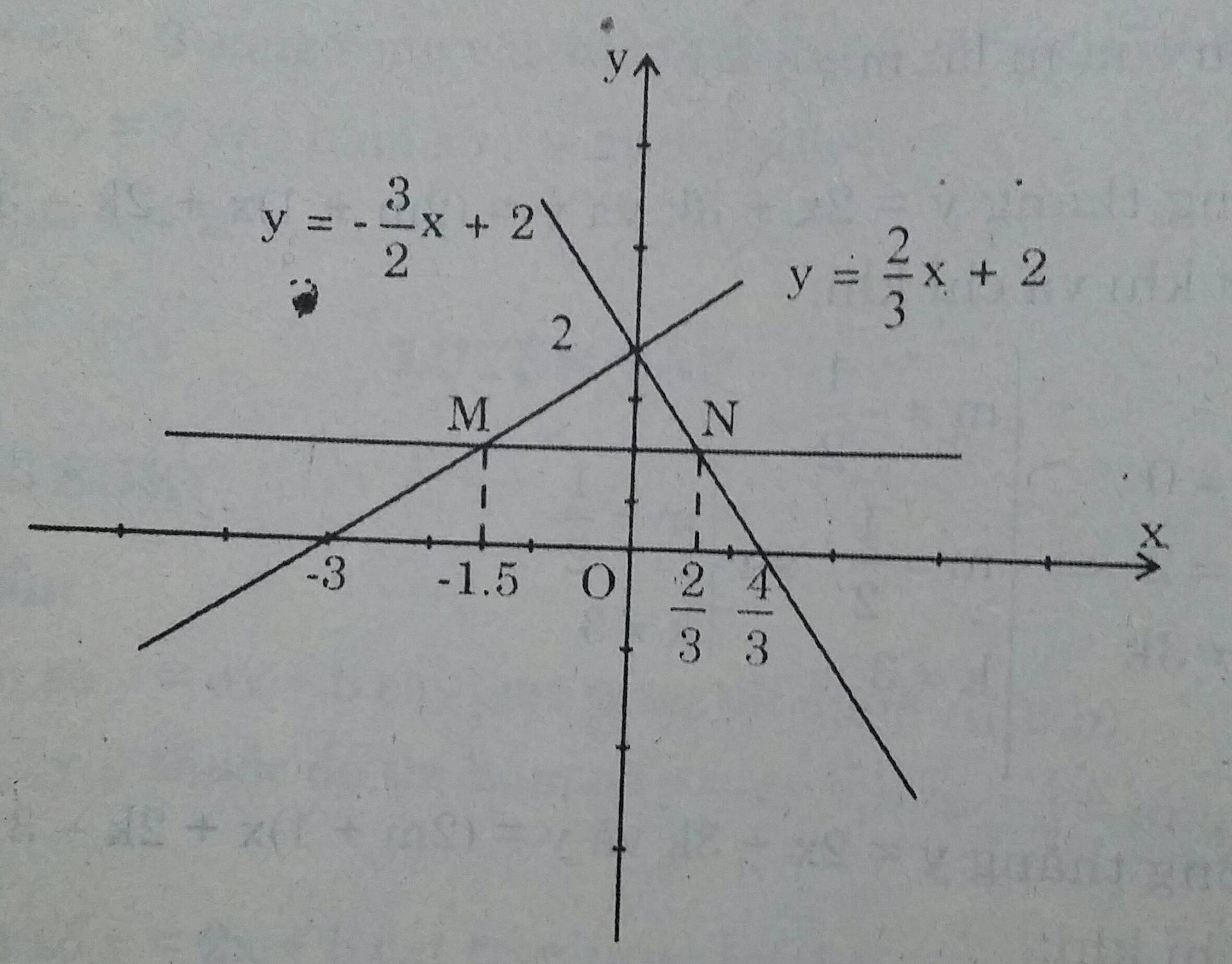
   b) Đường thẳng song song với trục hoành Ox và cắt trục tung tại điểm có tung độ bằng 1 có dạng y =1.

   Tọa độ giao điểm M của đường thẳng y=1 và đường thẳng \(y= \frac{2}{3}x+2 \) là nghiệm của phương trình: \( \frac{2}{3}x+2 =1 ​​\Leftrightarrow x=- \frac{3}{2}\)

   Vậy  \(M ( - \frac{3}{2}; 1) \)

 Tọa độ giao điểm N của đường thẳng y=1 và đương thẳng \(y=- \frac{2}{3}x+2 \) là nghiệm của phương trình \( - \frac{2}{3}x+2 =1 \Leftrightarrow x = \frac{2}{3}\)

  Vậy \(N (\frac{2}{3};1)\)