5. Giải bài 18 trang 110 - Sách giáo khoa Toán 9 tập 1

Giải bài 18 trang 110 - Sách giáo khoa Toán 9 tập 1

Đề bài

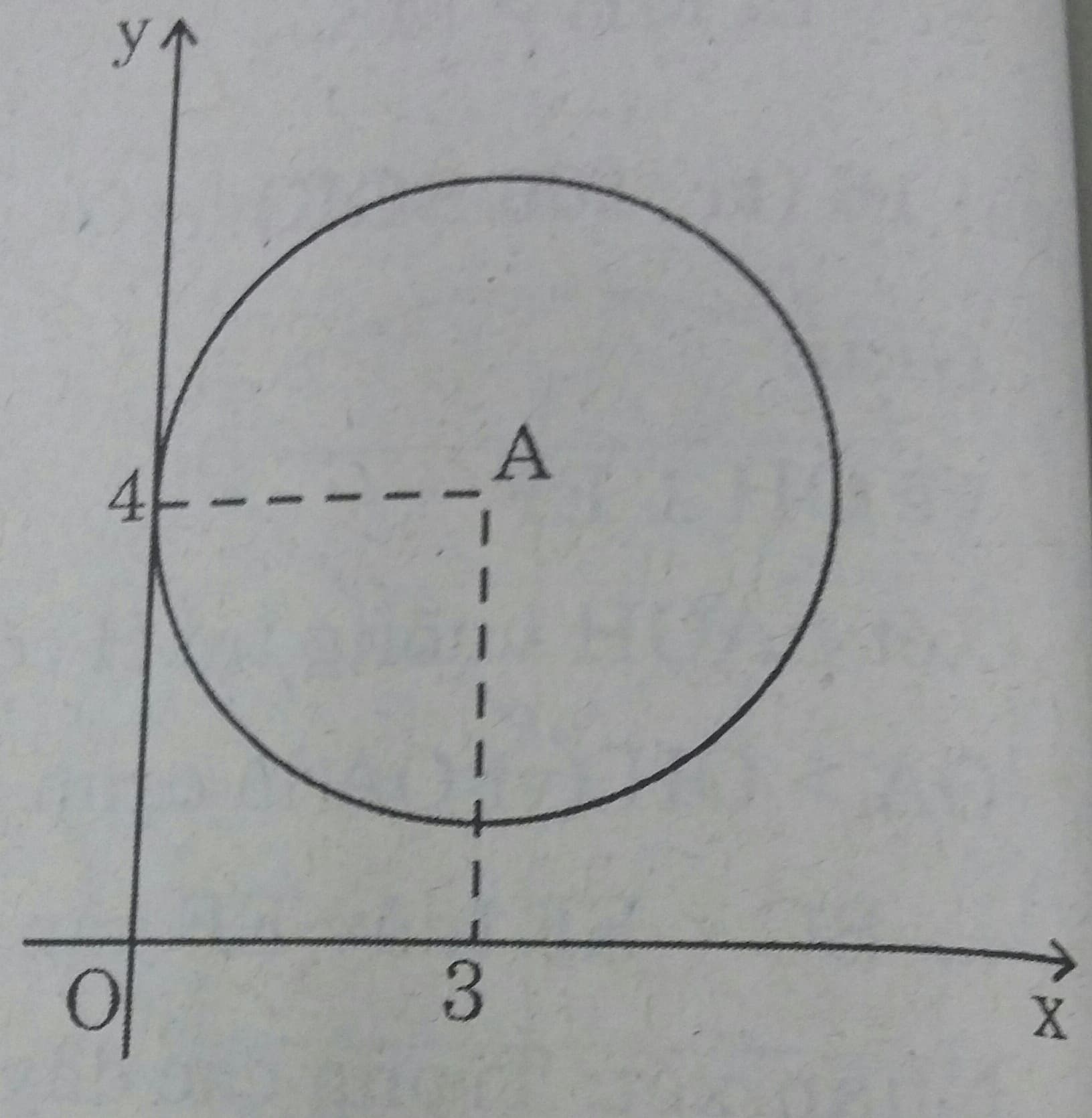
   Trên mặt phẳng tọa độ Oxy, cho điểm A(3; 4). Hãy xác định vị trí tương đối của đường tròn (A; 3) và các trục tọa độ.

Hướng dẫn giải

   Khoảng cách từ điểm A đến trục Ox là d= 4 > R \( \Rightarrow \) đường tròn ( A; 3) và trục Ox không cắt nhau. 

  Khoảng cách từ điểm A đến trục Oy là d'=3 = R \( \Rightarrow \) đường tròn ( A; 3) tiếp xúc với  trục Ox . 

   

 

Bạn muốn xem thêm với

Có thể bạn quan tâm

Giải bài 17 trang 109 - Sách giáo khoa Toán 9 tập 1

    R d Vị trí tương đối của đường thẳng và đường tròn 5cm  3cm  Đường thẳng cắt đường tròn. 6cm 6cm Tiếp xúc nhau. 4cm 7cm  Đường thẳng và đường tròn không cắt nhau.  

Giải bài 16 trang 106 - Sách giáo khoa Toán 9 tập 1

     Vẽ OH perp EF     Xét Delta AOH  vuông tại H có:     OA> OH Vì OA là cạnh huyền, OH là cạnh góc vuông    Rightarrow BC < EF   Dây EF gần tâm hơn thì lớn hơn     Nhận xét: Trong các dây đi qua một điểm A nằm trong đường tròn, dây vuông góc với bán kính qua A là dây ngắn nhất. 

Giải bài 15 trang 106 - Sách giáo khoa Toán 9 tập 1

     HƯỚNG DẪN:   Dây nào gần tâm hơn thì lớn hơn và ngược lại:      GIẢI:       a Xét đường trong nhỏ:   có AB> CD  Rightarrow OH < OK   Vì dây  AB lớn hơn thì gần tâm hơn      b Xét đường tròn lớn:   Có OH < OK  Rightarrow ME > MF  vì dây ME gần tâm hơn thì lớn hơn      c Có ME> MF mà MH =

Giải bài 14 trang 106 - Sách giáo khoa Toán 9 tập 1

   HƯỚNG DẪN:    Kẻ OH perp AB,   OH cắt CD tại K, ta có HA= HB và KC =KD.   Áp dụng định lí Pytago cho các tam giác vuông OHA và OKC tính được OH và KC từ đó tính CD.    GIẢI:    Kẻ OH perp AB , OH cắt CD tại K , thì OK perp CD  vì AB // CD   Ta có:      HA= HB = frac{1}{2}AB= frac{1}{2

Giải bài 1 trang 88 - Sách giáo khoa Toán 7 tập 2

a Đặt A = 9,6.2dfrac{1}{2}2.1251dfrac{5}{12}:dfrac{1}{4}=9,6.dfrac{5}{2}250dfrac{17}{12}.4               = 24 dfrac{2983}{12}.4 = 24 dfrac{2983}{3}=dfrac{2911}{3} b Đặt B = dfrac{5}{18}1,456:dfrac{7}{25}+4,5.dfrac{4}{5}=dfrac{5}{18}1,456.dfrac{25}{7}+3,6               = dfra

Giải bài 19 trang 110 - Sách giáo khoa Toán 9 tập 1

      Đường tròn O tiếp xúc với đường thẳng xy  Rightarrow  d= R =1cm.      Vậy O nằm trên hai đường thẳng a và a' cố định, song song với xy và cách xy một khoảng không đổi băng 1 cm.    

Giải bài 20 trang 110 - Sách giáo khoa Toán 9 tập 1

    OB là  bán kinh đi qua tiếp điểm  Rightarrow OB perp AB     Áp dụng định lí Py tago cho tam giác vuông OBA, ta có     AB = sqrt{OA^2OB^2}= sqrt{10^26^2}= 8cm

Giải bài 21 trang 111 - Sách giáo khoa Toán 9 tập 1

   Ta có: 3^2+ 4^2=5^2 Rightarrow AB^2+ AC^2= BC^2   Theo định lí Pytago đảo thì Delta ABC  vuông tại A  Rightarrow CA perp BA   Vậy CA là tiếp tuyến của đường tròn B.