Bài 20 trang 110 SGK Toán 9 tập 1

Đề bài

Cho đường tròn tâm \(O\) bán kính \(6cm\) và một điểm \(A\) cách \(O\) là \(10cm\). Kẻ tiếp tuyến \(AB\) với đường tròn (\(B\) là tiếp điểm). Tính độ dài \(AB\).

Hướng dẫn giải

+) Nếu một đường thẳng là tiếp tuyến của đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.

+) Sử dụng định lí Pytago: \(\Delta{ABC}\) vuông tại \(A\) thì \(BC^2=AC^2+AB^2\).

Lời giải chi tiết

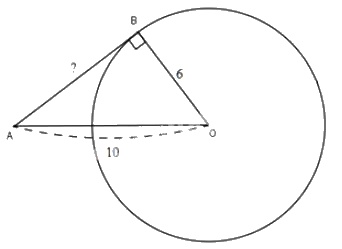
Vì \(B\) là tiếp điểm nên \(OB=R=6cm\).

Vì \(AB\) là tiếp tuyến tại \(B\) nên \(AB \bot OB\) tại \(B\). 

Xét \(\Delta{ABO}\) vuông tại \(B\), áp dụng định lý Pytago, ta có:

\(OA^2=OB^2+AB^2 \Leftrightarrow AB^2=AO^2-OB^2\)

\(\Leftrightarrow AB^2=10^2-6^2=100-36=64\)

\(\Leftrightarrow AB=\sqrt{64}=8(cm)\)