Đề kiểm tra 45 phút (1 tiết) - Đề số 7 - Chương 2 - Hình học 9

Đề bài

Cho ∆ABC vuông tại A. Vẽ đường tròn (O) qua A và tiếp xúc với BC tại B. Vẽ đường tròn (O’) qua A và tiếp xúc với BC tại C.

a. Chứng minh rằng (O) và (O’) tiếp xúc nhau tại A.

b. Gọi I là trung điểm của BC. Chứng minh rằng : \(\widehat {OIO'} = 90^\circ \) và \(AI ⊥ OO’\).

c. Tính các cạnh của ∆ABC biết bán kính của hai đường tròn là R và R’.

Hướng dẫn giải

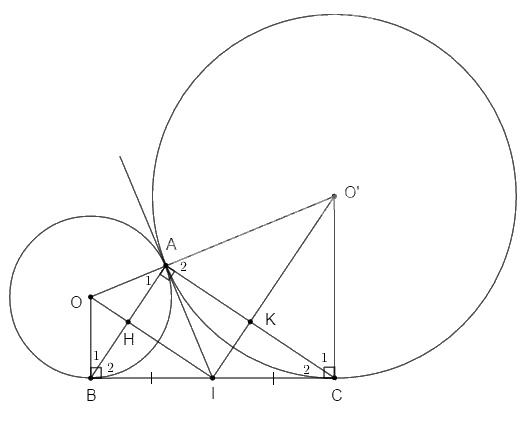
a. (O) và (O’) tiếp xúc với BC tại B và C nên \(OB ⊥ BC\) và \(O’C ⊥ BC\)

hay \({\widehat B_1} + {\widehat B_2} + {\widehat C_1} + {\widehat C_2} = 180^\circ ,\)

mà \({\widehat B_2} + {\widehat C_2} = 90^\circ \) (do ∆ABC vuông tại A) \( \Rightarrow {\widehat B_1} + {\widehat C_1} = 90^\circ \)

∆BOA và ∆CO’A cân tại O và O’ nên.

\(\eqalign{  & {\widehat B_1} = {\widehat A_1},{\widehat C_1} = {\widehat A_2}  \cr  &  \Rightarrow {\widehat A_1} + {\widehat A_2} = 90^\circ  \cr} \)

Do đó \({\widehat A_1} + \widehat {BAC} + {\widehat A_2} = 180^\circ \)

Vậy ba điểm O, A, O’ thẳng hàng.

Mặt khác : \(OO’ = OA + AO’\)

nên (O) và (O’) tiếp xúc nhau tại A.

b. I là trung điểm của BC (gt) nên AI là trung tuyến của ∆ABC vuông tại A \(⇒ IA = IB = IC.\)

Do đó \(∆IAO = ∆IBO\) (c.c.c) \( \Rightarrow \widehat {IAO} = \widehat {IBO} = 90^\circ \)

⇒ AI là tiếp tuyến của (O) và (O’). Do đó IO và IO’ là phân giác của các góc kề bù AIB và AIC \( \Rightarrow \widehat {OIO'} = 90^\circ \)

Cách khác : Ta có: \(IA = IB, OA = OB ⇒ OI\) là trung trực của AB

\(⇒ OI ⊥ AB\) hay \(\widehat {AHI} = 90^\circ \) (H là giao điểm của OI và AB).

Chứng minh tương tự có \(\widehat {AKI} = 90^\circ \) (K là giao điểm của O’I và AC) nên AHIK là hình chữ nhật \( \Rightarrow \widehat {OIO'} = 90^\circ \)

c. ∆OIO’ vuông có AI là đường cao ta có:

\(A{I^2} = AO.AO' \Rightarrow AI = \sqrt {R.R'} \). Do đó: \(BC = 2\sqrt {R.R'} \)

Gọi H là giao điểm của OI và AB. ∆OAI vuông tại A (cmt) có AH là đường cao, ta có:

\({1 \over {A{H^2}}} = {1 \over {A{O^2}}} + {1 \over {A{I^2}}}\) (định lí 4)

hay

\(\eqalign{  & {1 \over {A{H^2}}} = {1 \over {{R^2}}} + {1 \over {{{\left( {\sqrt {R.R'} } \right)}^2}}} \cr&\;\;\;\;\;\;\;\;\;\;= {1 \over {{R^2}}} + {1 \over {R.R'}} = {{R' + R} \over {{R^2}R'}}  \cr  &  \Rightarrow AH = R\sqrt {{{R'} \over {R + R'}}} \cr& \Rightarrow AB = 2AH = 2R\sqrt {{{R'} \over {R + R'}}}  \cr} \)

Tương tự \(AC = 2R'\sqrt {{R \over {R + R'}}} \)