Giải bài 42 trang 128 - Sách giáo khoa Toán 9 tập 1
Đề bài
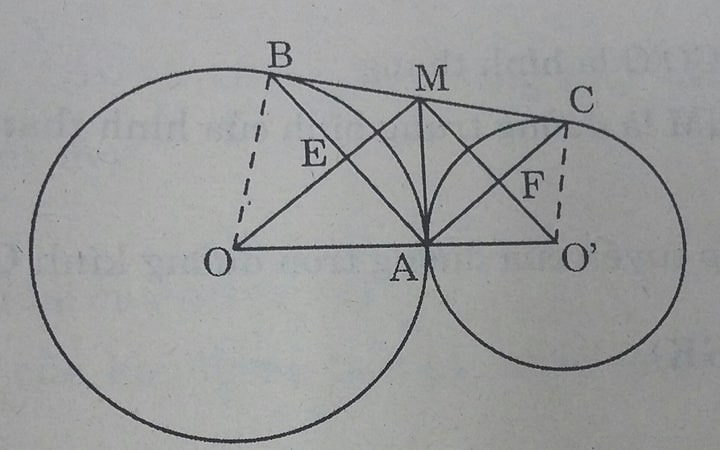
Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A, BC là tiếp tuyến chung ngoài, B ∈ (O), C ∈ (O'). Tiếp tuyến chung trong tại A cắt BC ở điểm M. Gọi E là giao điểm của OM và AB, F là giao điểm của O'M và AC. Chứng minh rằng:
a) Tứ giác AEMF là hình chữ nhật.
b) ME.MO = MF.MO'
c) OO' là tiếp tuyến của đường tròn có đường kính là BC
d) BC là tiếp tuyến của đường tròn có đường kính OO'
Hướng dẫn giải
Giải:
a) MA, MB là hai tiếp tuyến cắt nhau \( \Rightarrow ME \perp AB \Rightarrow \widehat{MEA}= 90^0\)
MA, MC à hai tiếp tuyến cắt nhau \( \Rightarrow MF \perp AC \Rightarrow \widehat{MFA}= 90^0\)
Mặt khác MO và MO' theo thứ tự là tia phân giác của các góc \( \widehat{AMB} \ và \ \widehat{AMC}\) ( tính chất của hai tiếp tuyến cắt nhau)
\( \Rightarrow MO \perp MO' \) ( hai tia phân giác của hai góc kề bù) \( \Rightarrow \widehat{EMF}=90^0\)
Vậy tứ giác AEMF là hình chữ nhật vì có 3 góc vuông.
b) Xét \(\Delta AOM \) vuông tại A có \(AE \perp OM \ có \ ME.MO= AM^2\)
Tương tự ta có: MF. MO' =\(AM^2\)
Suy ra: \(ME.MO= MF.MO'\)
c) Ta có MA= MB= MC suy ra đường tròn đường kính BC đi qua A.
Mặt khác \(OO'\perp MA\) ( tính chất tiếp tuyến) \( \Rightarrow OO'\) là tiếp tuyến của đường tròn đường kính BC.
d) Gọi \(I\) là trung điểm OO' \(\Rightarrow I \) là tâm đường tròn đường kính OO'.
Ta có \(\Delta MOO'\) vuông tại M nên đường tròn đường kính OO' đi qua M.
Ta có \(OB \perp BC \ và \ O'C \perp BC \) ( tính chất tiếp tuyến)
\( \Rightarrow OB \) // O'C
\(\Rightarrow\) Tứ giác BCO'O là hình thang
\(\Rightarrow\) IM// OB ( IM là đường trung bình của hình thang)
\(\Rightarrow\) \(IM \perp BC\)
Vậy BC là tiếp tuyến của đường tròn đường kính OO'.

