Đề kiểm tra 45 phút (1 tiết) - Đề số 6 - Chương 2 - Hình học 9
Đề bài
Cho đường tròn (O) đường kính BC. Dây \(AD ⊥ BC\) tại H. Gọi E, F theo thứ tự là chân các đường vuông góc kẻ từ H đến AB và AC. Gọi (I), (K) là các đường tròn ngoài tiếp các tam giác HBE và HCF.
a. Xác định vị trí tương đối của các đường tròn (I) và (O); (K) và (O); (I) và (K).
b. Chứng minh: \(AE.AB = AF.AC.\)
c. Chứng minh rằng EF là tiếp tuyến chung của đường tròn (I) và (K).
d. Xác định vị trí điểm H để EF có độ dài lớn nhất.
Hướng dẫn giải
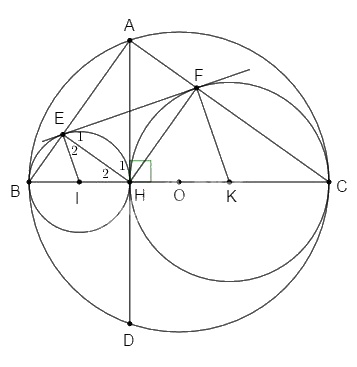
a. Ta có: \(IO = OB – IB\; (d = R – R_1)\)
\(⇒ (I)\) và \((O)\) tiếp xúc trong tại B.
Chứng minh tương tự ta có: (K) và (O) tiếp xúc trong tại C.
\(IK = IH + HK \;(d = R_1+R_2)\)
\(⇒ (I)\) và \((K)\) tiếp xúc ngoài tại H.
b. ∆AHB vuông tại H có HE là đường cao, ta có: \(A{H^2} = AE.AB\)
Tương tự với tam giác vuông AHC ta có:
\(A{H^2} = AF.AC\)
Do đó: \(AE.AB = AF.AC\)
c. Các tam giác ABC, BEH, CFH vuông vì chắn nửa đường tròn có đường kính lần lượt là BC, BH, CH. Do đó tứ giác AEHF là hình chứ nhật (có 3 góc vuông) \( \Rightarrow {\widehat E_1} = {\widehat H_1}\)
Mặt khác ∆EIH cân nên \({\widehat E_2} = {\widehat H_2},\) mà \(\,{\widehat H_1} + {\widehat H_2} = 90^\circ \) (gt)
\( \Rightarrow {\widehat E_1} + {\widehat E_2} = 90^\circ \,hay\,EF \bot IE\)
Tương tự ta chứng minh được \(EF ⊥ KF\). Vậy EF là tiếp tuyến chung của đường tròn (I) và (K).
d. Do AEHF là hình chữ nhật (cmt) \(⇒ EF = AH\) nên EF có độ dài lớn nhất khi AH có độ dài lớn nhất. \(AH ≤ OA = R\) (không đổi). Dấu “=” xảy ra khi \(H ≡ O\). Vậy khi H trùng với O thì AH có độ dài lớn nhất là R.

