Đề kiểm tra 45 phút (1 tiết) - Đề số 10 - Chương 2 - Hình học 9

Đề bài

Bài 1. Cho đường tròn (O) nội tiếp ∆ABC. Gọi M, N, S lần lượt là các tiếp điểm thuộc các cạnh AB, BC, CA. Chứng minh rằng :

\(AB + AC – BC = 2AM.\)

Bài 2. Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm A và B. Một cát tuyến kẻ qua A cắt (O) tại C và cắt (O’) tại D. Gọi H, K lần lượt là trung điểm của AC và AD và I là trung điểm của HK.

a. Chứng minh rằng đường thẳng vuông góc với CD tại I đi qua một điểm cố định P khi cát tuyến CAD thay đổi.

b. Kẻ đường thẳng vuông góc với PA tại A, đường thẳng này cắt (O) tại E và cắt (O’) tại F. Chứng minh : \(AE = AF.\)

c. Gọi AR, AQ lần lượt là đường kính của (O) và (O’). Chứng minh R, B, Q thẳng hàng.

Hướng dẫn giải

Bài 1.

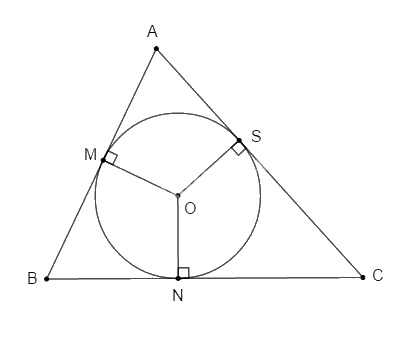
Ta có: \(AB + AC – BC \)\(\,= AM + MB + AS + SC – BN – NC\)

Mà \(AM = AS, MB = NB, CS = NC\) (tính chất tiếp tuyến cắt nhau)

\(⇒ AB + AC – BC \)\(\,= AM + AS = 2AM.\)

Bài 2.

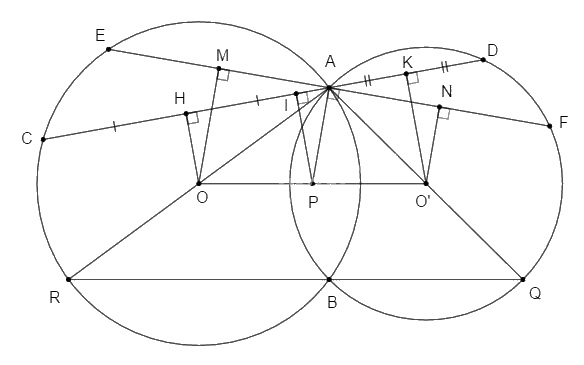
a. Ta có: H, K lần lượt là trung điểm của AC và AD (gt) nên \(OH ⊥ AC\) và \(O’K ⊥ AD\) (định lí đường kính dây cung). Do đó tứ giác OHKO’ là hình thang vuông.

Gọi P là giao điểm của OO’ và đường thẳng qua I vuông góc với CD, ta có: IP là đường trung bình của hình thang OHKO’ \(⇒ P\) là trung điểm của OO’ nên P cố định.

b. Kẻ OM, O’N lần lượt vuông góc với EF. Ta có OMBO’ là hình thang vuông có PA là đường trung bình nên A là trung điểm của MN hay \(AM = AN ⇒ AE = AF.\)

c. Dễ thấy \(\widehat {ABR} = \widehat {ABQ} = 90^\circ \) (chắn các nửa đường tròn)

\( \Rightarrow \widehat {RBA} + \widehat {ABQ} = 180^\circ \) \(⇒\) Ba điểm R, B, Q thẳng hàng.