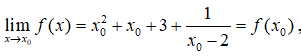Chuyên đề về hàm số liên tục và bộ bài tập có lời giải
Chuyên đề về hàm số liên tục và bộ bài tập có lời giải
Hàm số liên tục là dạng bài tập khá phổ biến và xuất hiện ở hầu hết các đề thi. Được đánh giá là một học phần khá quan trọng trong chương trình đại số và giải tích bậc trung học phổ thông, các bạn phải nắm chắc những kiến thức từ cơ bản đến chi tiết về nó. Bài viết sau sẽ đưa ra cho bạn câu trả lời hợp lý!
I. Hàm số liên tục
1. Hàm số liên tục là gì?
Hàm f gọi là liên tục tại điểm c trên miền xác định nếu giới hạn của f(x) khi x tiến dần về c tồn tại và bằng giá trị của f(c). Ta viết:
\({\displaystyle {\underset {x\rightarrow c}{\lim }}f(x)=f(c)}\)hay chính là 3 điều kiện sau: 1 là f xác định tại c, 2 là giới hạn bên vế trái là tồn tại, thứ 3 là giá trị của giới hạn phải bằng f(c).
Hàm f là liên tục nếu liên tục tại mọi điểm trong miền xác định.
Ví dụ: Hàm \( {\displaystyle f(x)={\frac {2x-1}{x+2}}} \) liên tục trên miền xác định \({\displaystyle \mathbb {R\backslash } \{-2\}}\)
Công thức liên quan:
2. Xét tính liên tục của hàm số
- Xét tính liên tục tại 1 điểm: y = f(x) liên tục tại \(x_0 \iff \mathop {\lim }\limits_{x \to {x_0}} f(x) = f({x_0})\)
Để xét tính liên tục của y = f(x) tại xo ta thực hiện các bước sau:
Bước 1: Tính f(xo)
Bước 2: Tính \(\lim\limits_{x \to {x_0}}\) trong nhiều trường hợp ta cần tính \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x)\), \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x)\)
Bước 3: So sánh \(\mathop {\lim }\limits_{x \to {x_0} } f(x_o)\) với f(xo) và rút ra kết luận.
Bước 4: Kết luận
- Xét tính liên tục trên một khoảng: y = f(x) liên tục tại mọi điểm thuộc khoảng đó.
- Xét tính liên tục trên một đoạn [a;b]: y = f(x) liên tục trên (a;b) và \(\mathop {\lim }\limits_{x \to {a}^ + } f(x)=f(a)\), \(\mathop {\lim }\limits_{x \to {b}^ - } f(x)=f(b)\).
- Hàm số đa thức liên tục trên R: hàm số phân thức, các hàm số lượng giác liên tục trên từng khoảng xác định của chúng.
III. Bài tập hàm số liên tục có lời giải
Bài 1: Chứng minh rằng :
Hàm số \(f(x)=x^4−x^2+2\) liên tục trên R.
Lời giải:
Hàm số \(f(x)=x^4−x^2+2\) xác định trên R, \(\forall x\in R\) ta có:
\(\mathop {\lim }\limits_{x \to {x_0}} = \mathop {\lim }\limits_{x \to {x_0}} \left( {{x^4} - {x^2} + 2} \right) = x_0^4 - x_0^2 + 2 = f\left( {{x_0}} \right)\)
Vậy f liên tục tại xo nên f liên tục trên R.
Bài 2: Chứng minh rằng hàm số \(f\left( x \right) = {x^2} + x + 3 + {1 \over {x - 2}}\) liên tục trên tập xác định của nó.
Lời giải:
Tập xác định D = R\{2}
Với mọi xo ≠ 2, ta có:
suy ra f liên tục tại mọi xo ≠ 2 nên f liên tục trên tập xác định
Với những kiến thức tổng hợp trên hy vọng rằng nó đã giúp bạn giải đáp phần nào cách làm dạng bài này. Để học tập thật tốt hãy đầu tư thời gian vào làm bài cũng như trau dồi các kiến thức hôn nhé. Chúng tôi tin chắc rằng chúng sẽ không làm khó được bạn. Chúc các bạn thành công!