Bài 59 trang 90 SGK Toán 9 tập 2

Đề bài

Cho hình bình hành \(ABCD.\) Đường tròn đi qua ba đỉnh \(A, \, B, \, C\) cắt đường thẳng \(CD\) tại \(P\) khác \(C.\) Chứng minh \(AP = AD.\)

Hướng dẫn giải

+) Số đo tổng hai góc đối diện của tứ giác nội tiếp bằng \(180^0.\)

Lời giải chi tiết

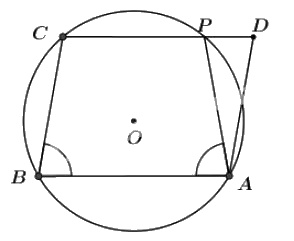
Do tứ giác \(ABCP\) nội tiếp nên ta có:

             \(\widehat{BAP} + \widehat{BCP} = 180^0.\)        (1)

Ta lại có: \(\widehat{ABC}+ \widehat{BCP}=  180^0\) (hai góc trong cùng phía do \(CD//AB\)).      (2)

Từ (1) và (2) suy ra: \(\widehat{BAP}= \widehat{ABC}.\)

Vậy \(ABCP\) là hình thang cân, suy ra \(AP = BC.\)      (3)

Mà \(BC = AD\) (hai cạnh đối đỉnh của hình bình hành)  (4)

Từ (3) và (4) suy ra \(AP = AD.\) (đpcm).