Giải bài 63 trang 92 - Sách giáo khoa Toán 9 tập 2

Đề bài

   Vẽ hình lục giác đều, hình vuông, tam giác đều cùng nội tiếp đường tròn (O; R) rồi tính cạnh của các hình đó theo R.

Hướng dẫn giải

   a) Vẽ hình lục giác đều nội tiếp.

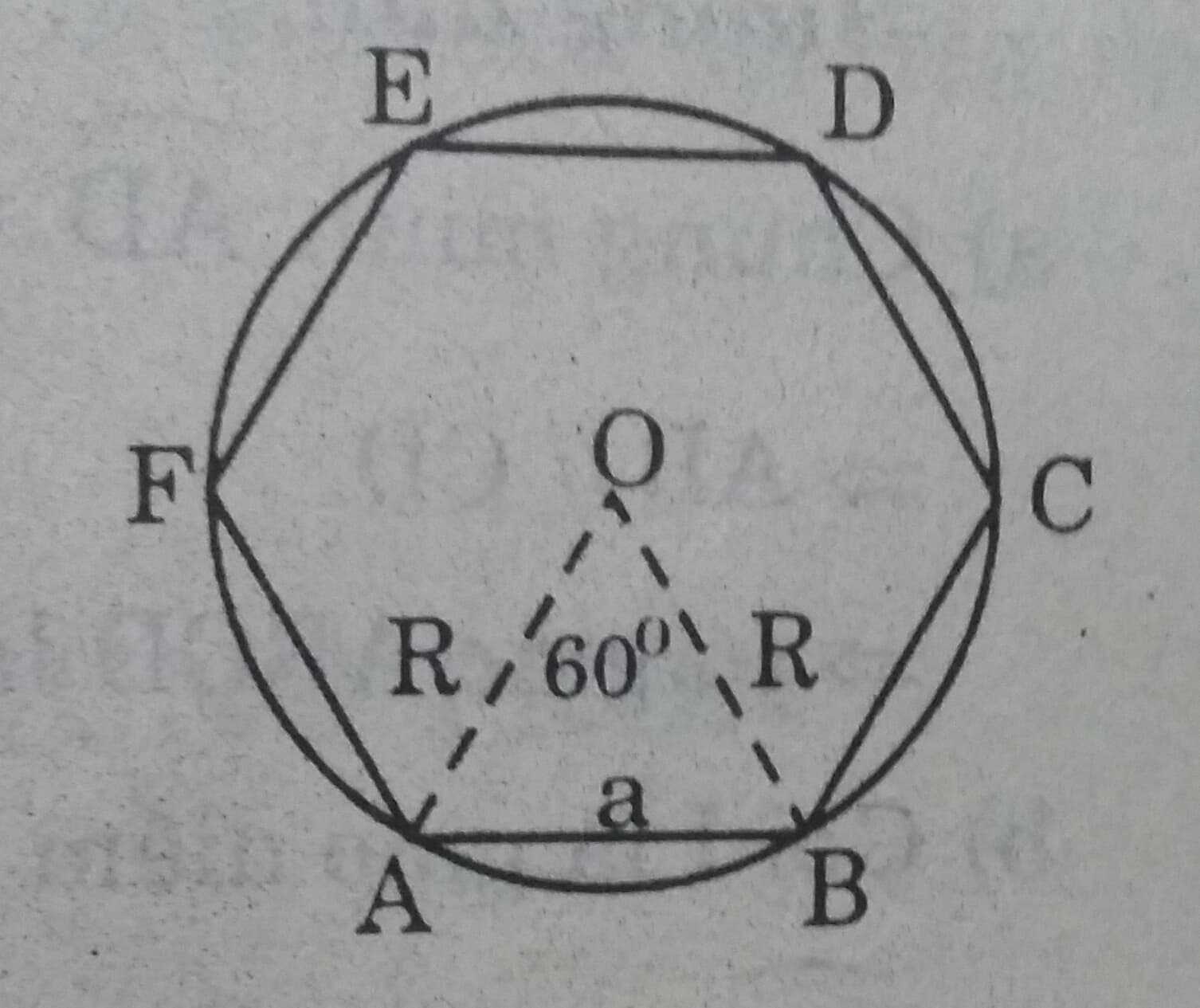
  Cách vẽ: Dựng 6 góc ở tâm có số đo bằng nhau, mỗi góc có số đo là \(60^0 \) góc này chia đường tròn thành sáu cung bằng nhau.

   Tính độ dài mỗi cạnh:

   \(\Delta AOB \) là tam giác cân có \(\widehat{AOB}= 60^0 \Rightarrow \Delta AOB \ là \ tam \ giác \ đều,\)

 Do đó a = AB = R

  b) Vẽ hình vuông nội tiếp

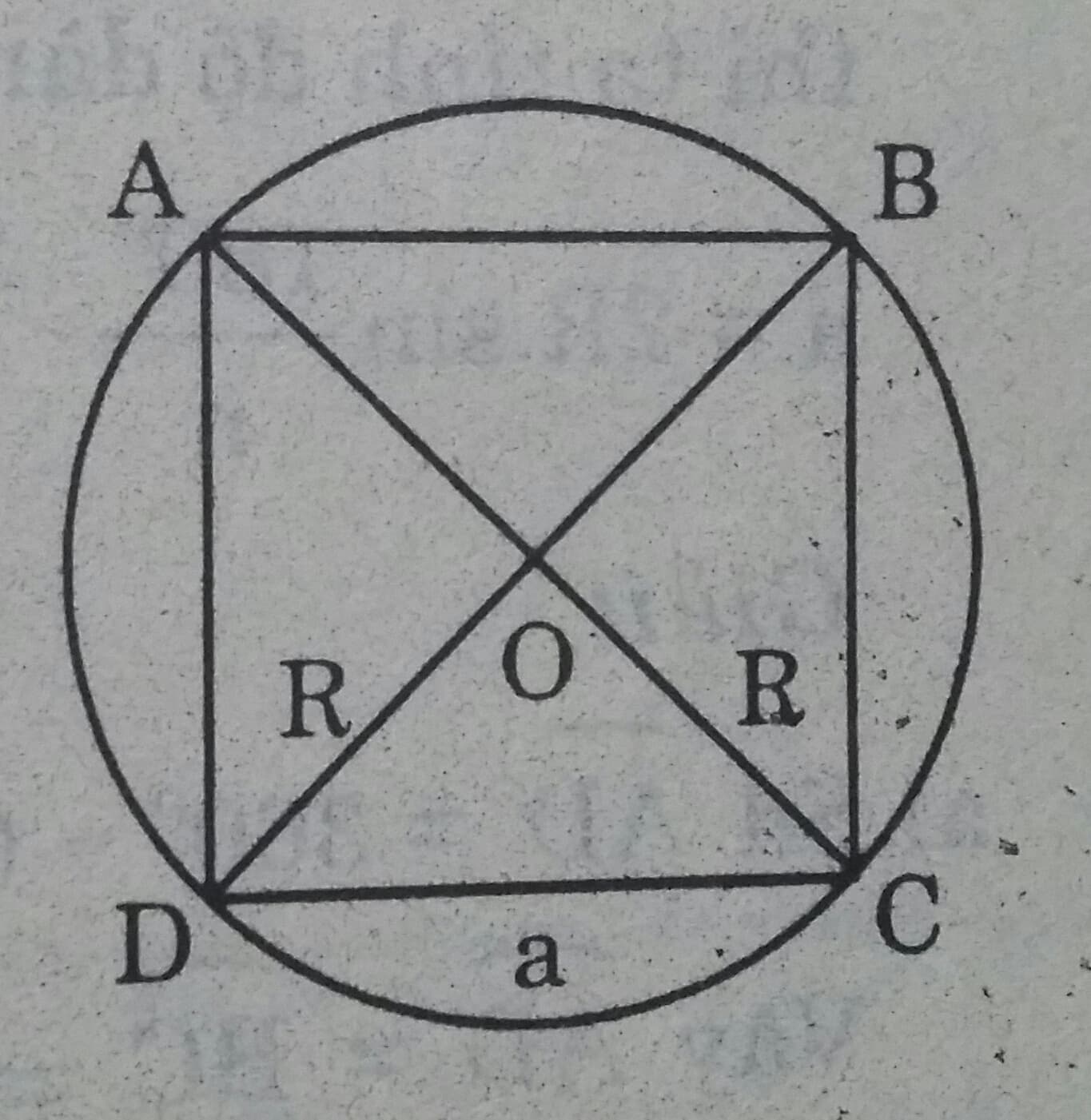
  Cách vẽ: Vẽ hai đường kính AC và BD vuông góc với nhau. Vẽ các dây AB, BC, CD, DA ta được tứ giác ABCD là hình vuông nội tiếp đường tròn.

   Tính độ dài mỗi cạnh:

  \(\Delta COD\) vuông cân nên

  \(CD^2 = OC^2 + OD^2 \Rightarrow a^2 = 2R^2 \Rightarrow a = R \sqrt{2}\)

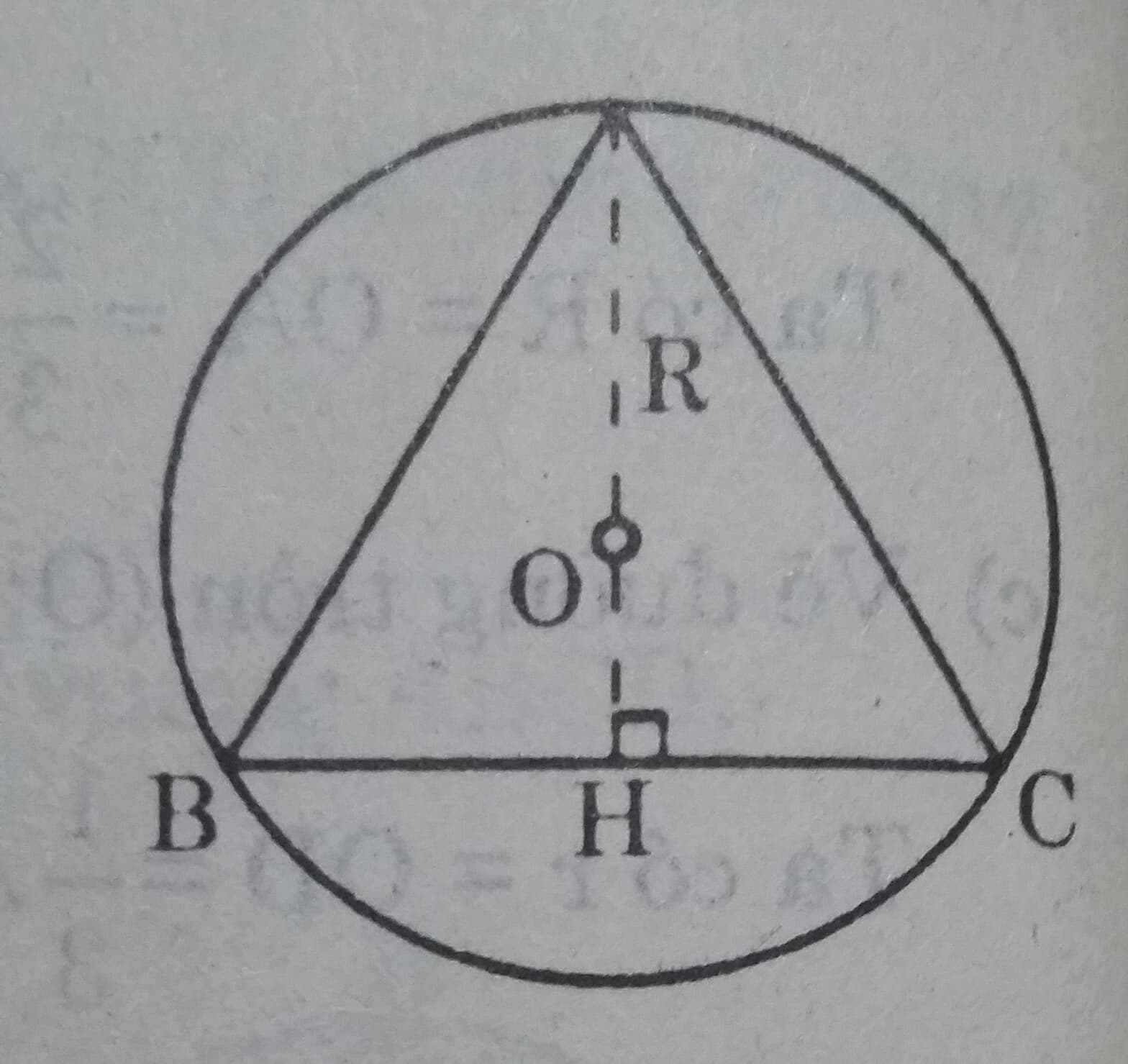
  c) Vẽ tam giác đều nội tiếp.

  Cách vẽ: Chia đường tròn làm 6 cung bằng nhau. Nối các điểm chia cách nhau một điểm ta được tam giác đều.

  Tính độ dài mỗi cạnh:

  Xét tam giác HAB vuông tại H có:

   \( AH = \dfrac{2}{3}R\\AH = AB.Sin\widehat{B} \Rightarrow AB= \dfrac{AH}{Sin\widehat{B}}= \dfrac{ \dfrac{3}{2}R}{ \dfrac{\sqrt{3}}{2}}\\ \Rightarrow a = R \sqrt{3}\)