Bài 58 trang 90 SGK Toán 9 tập 2

Đề bài

Cho tam giác đều $ABC.$ Trên nửa mặt phẳng bờ $BC$ không chứa đỉnh $A,$ lấy điểm $D$ sao cho $DB = DC$ và $\widehat{DCB}=\frac{1}{2}\widehat{ACB}.$

a) Chứng minh $ABDC$ là tứ giác nội tiếp.

b) Xác định tâm của đường tròn đi qua bốn điểm $A,\, B,\, D, \,C$.

Hướng dẫn giải

+) Tứ giác có tổng hai góc đối diện bằng $180^0$ thì tứ giác đó là tứ giác nội tiếp.

Lời giải chi tiết

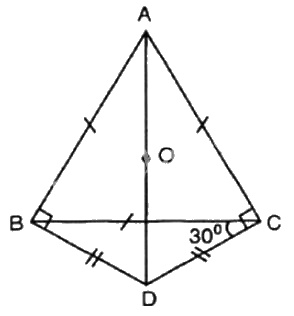
a) Theo giả thiết, $\widehat{DCB}=\frac{1}{2}\widehat{ACB} = \frac{1}{2} .60^0= 30^0.$  

 $\widehat{ACD}=\widehat{ACB} +\widehat{BCD}$ (tia $CB$ nằm giữa hai tia $CA,\, CD$)

$\Rightarrow$$\widehat{ACD}=60^0+ 30^0=90^0$  (1)

Do $DB = CD$ nên $∆BDC$ cân tại $D$ $\Rightarrow \widehat{DBC} = \widehat{DCB} = 30^0$

Từ đó $\widehat{ABD}= 30^0+60^0=90^0$ (2)

Từ (1) và (2) có $\widehat{ACD}+ \widehat{ABD}=180^0$ nên tứ giác $ABDC$ là tứ giác nội tiếp.

b) Vì $\widehat{ABD}  = 90^0$ nên $AD$ là đường kính của đường tròn ngoại tiếp tứ giác $ABDC,$ do đó tâm đường tròn ngoại tiếp tứ giác $ABDC$ là trung điểm $AD.$