Bài 43 trang 83 SGK Toán 9 tập 2
Đề bài
Cho đường tròn \((O)\) và hai dây cung song song \(AB,\, CD\) (\(A\) và \(C\) nằm trong cùng một nửa mặt phẳng bờ \(BD\)); \(AD\) cắt \(BC\) tại \(I\). Chứng minh \(\widehat{AOC }= \widehat{AIC }.\)
Hướng dẫn giải
+) Góc có đỉnh nằm ngoài đường tròn có số đo bằng nửa hiệu số đo hai cung bị chắn.
+) Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
Lời giải chi tiết
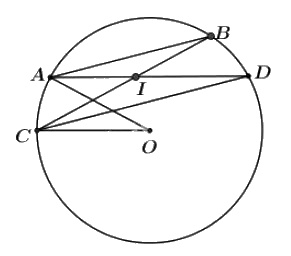
Theo giả thiết: \(\overparen{AC}=\overparen{BD}\) (vì \(AB // CD\)) (1)
Ta có: \(\widehat{AIC}\) là góc có đỉnh ở trong đường tròn chắn cung \(AC\) và cung \(BD\) \(\Rightarrow \widehat{AIC }= \frac{sđ\overparen{AC}+sđ\overparen{BD}}{2}\)
Theo (1) suy ra \(\widehat{AIC }= sđ\overparen{AC}\) (3)
Mà \(\widehat{AOC }= sđ\overparen{AC}\) (góc ở tâm chắn cung \(\overparen{AC}\)) (4)
So sánh (3), (4), ta có \(\widehat{AOC } = \widehat{AIC }\) (đpcm).

