Bài 28 trang 67 SGK Toán 7 tập 2
Đề bài
Cho tam giác DEF cân tại D với đường trung tuyến DI.
a) Chứng minh ∆DEI = ∆DFI.
b) Các góc DIE và góc DIF là những góc gì?
c) Biết DE = DF = 13cm, EF = 10cm, hãy tính độ dài đường trung tuyến DI.
Hướng dẫn giải
Áp dụng tính chất của tam giác cân, tính chất đường trung tuyến và định lý Pytago.
Lời giải chi tiết
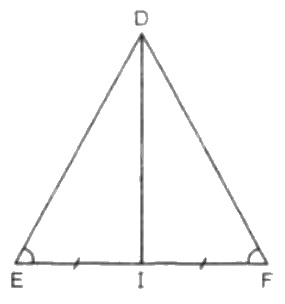
a) Xét ∆DEI và ∆DFI có:
DI là cạnh chung
DE = DF ( ∆DEF cân)
IE = IF (DI là trung tuyến)
Vậy ∆DEI = ∆DFI (c.c.c)
b) Vì ∆DEI = ∆DFI nên \(\widehat{DIE} =\widehat{DIF}\).
Mà \(\widehat{DIE} +\widehat{DIF}\) = 1800 ( hai góc kề bù)
\(\Rightarrow \) \(\widehat{DIE} =\widehat{DIF}\) = 900
Vậy các góc DIE và góc DIF là những góc vuông.
c) I là trung điểm của EF nên IE = IF = 5cm.
Áp dụng định lí Pytago trong ∆DEI vuông tại I ta có:
DE2 = DI2 + EI2
\(\Rightarrow \) DI2 = DE2 – EI2 = 132 – 52 = 144
\(\Rightarrow \) DI = 12 cm.

