Giải bài 30 trang 67 - Sách giáo khoa Toán 7 tập 2
Đề bài
Gọi G là trọng tâm của tam giác ABC. Trên tia AG lấy điểm G' sao cho G là trung điểm của AG'.
a) So sánh các cạnh của tam giác BGG' với các đường trung tuyến của tam giác ABC.
b) So sánh các đường trung tuyến của tam giác BGG' với các cạnh của tam giác ABC
Hướng dẫn giải
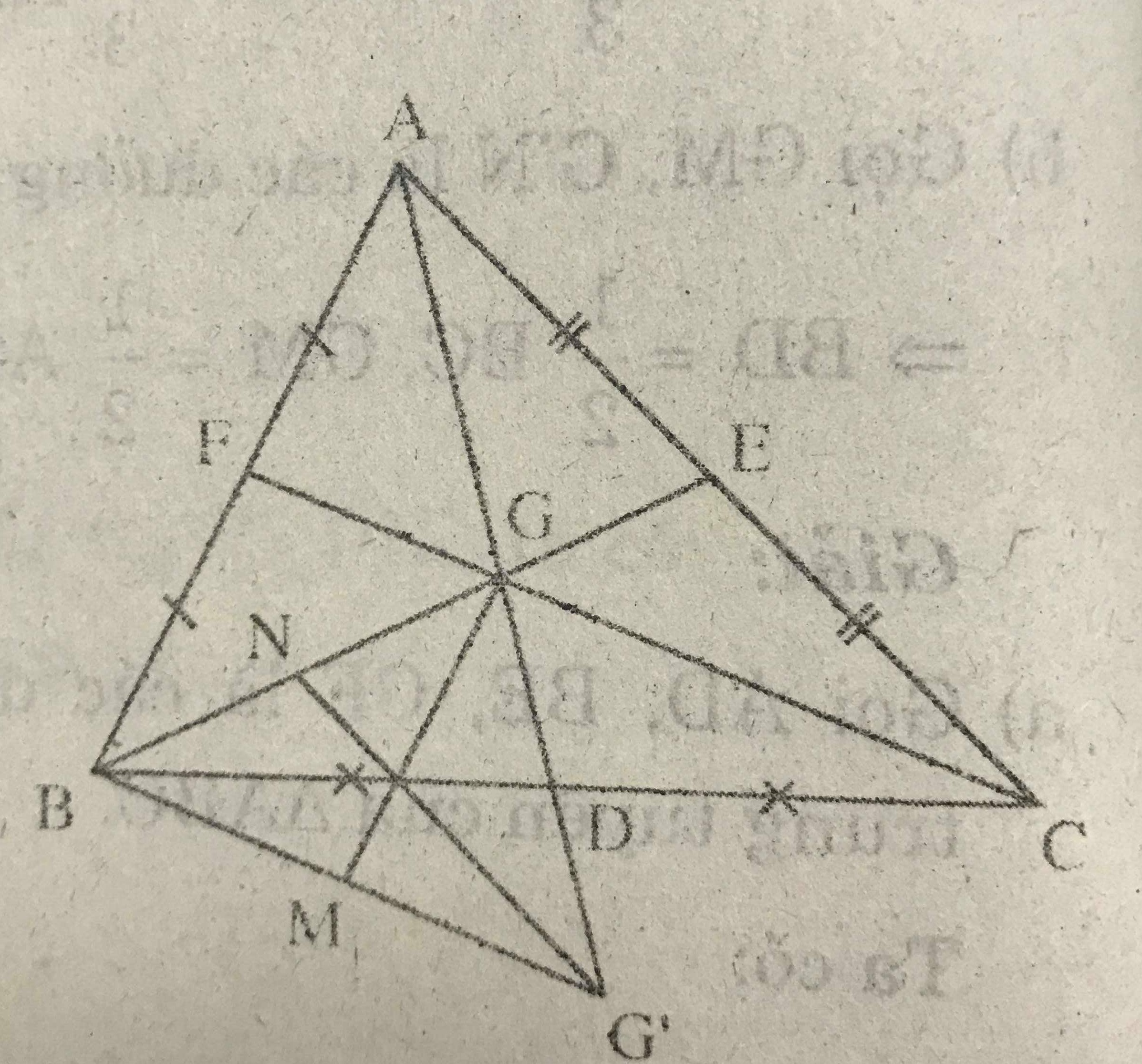
a) Gọi AD, BE, CF là các đường trung tuyến của ΔABC
Ta có :
BG = \(\dfrac{2}{3}\)BE (G là trọng tâm của ΔABC)
AG = \(\dfrac{2}{3}\)AD (G là trọng tâm của ΔABC)
Lại có GG' = AG (G là trung điểm của AG') nên GG' = \(\dfrac{2}{3}\)AD
G là trọng tâm của ΔABC => AG = 2GD => GG' = 2GD
=> GD = DG'
ΔBDG' và ΔCDG có :
DG = DG'
\(\widehat{BDG'}=\widehat{CDG}\) (hai góc đối đỉnh)
DB = DC (AD là đường trung tuyến của ΔABC)
Nên ΔBDG' = ΔCDG (c.g.c)
Suy ra BG' = CG (hai cạnh tương ứng của hai tam giác bằng nhau)
Lại có CG = \(\dfrac{2}{3}\)CF (tính chất trọng tâm)
Do đó BG' = \(\dfrac{2}{3}\)CF
Vậy các cạnh của ΔBGG' bằng \(\dfrac{2}{3}\) đường trung tuyến của ΔABC
b) DG = DG' => BD là đường trung tuyến của ΔBGG'
Ta có : BD = \(\dfrac{1}{2}\)BC (AD là đường trung tuyến của ΔABC)
Gọi GM và G'N là các đường trung tuyến của ΔBGG'
Ta có : MB = MG' ; GA = GG'
Nên MG là đường trung bình của ΔABG'
Suy ra MG = \(\dfrac{1}{2}\)AB
G'N là đường trung tuyến của ΔBGG' => NG = \(\dfrac{1}{2}\)BG
Lại có GE = \(\dfrac{1}{2}\)BG (tính chất trọng tâm)
Nên NG = GE
ΔNGG' và ΔEAG có :
NG = GE
GA = GG' (tính chất trung điểm)
\(\widehat{NGG'}=\widehat{EGA}\) (hai góc đối đỉnh)
Nên ΔNGG' = ΔEGA (c.g.c)
Suy ra G'N = AE (hai cạnh tương ứng)
Mà AE = \(\dfrac{1}{2}\)AC (BE là đường trung tuyến của ΔABC)
=> G'N = \(\dfrac{1}{2}\)AC
Vậy các đường trung tuyến của ΔBGG' bằng \(\dfrac{1}{2}\) cạnh của ΔABC.

