Bài 24 trang 123 SGK Toán 8 tập 1

Đề bài

Tính diện tích tam giác cân có cạnh đáy bằng \(a\) và cạnh bên bằng \(b.\)

Hướng dẫn giải

Áp dụng tính chất tam giác cân, định lí pitago, công thức tính diện tích tam giác.

Lời giải chi tiết

Gọi \(h\) là chiều cao của tam giác cân có đáy là \(a\) và cạnh bên là \(b.\)

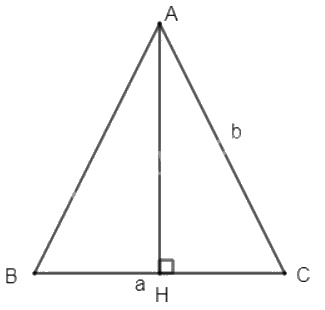
Vì \(\Delta ABC\) cân tại \(A\) (gt) nên \(AH\) vừa là đường cao vừa là đường trung tuyến (tính chất tam giác cân)

\( \Rightarrow BH = \frac{{BC}}{2} = \frac{a}{2}\)

Theo định lý Pitago ta có: 

\({h^2} = {b^2} - {\left( {\frac{a}{2}} \right)^2} = \frac{{4{b^2} - {a^2}}}{4} \)\(\Rightarrow h = \frac{{\sqrt {4{b^2} - {a^2}} }}{2}\)

\(S = \frac{1}{2}ah = \frac{1}{2}a.\frac{{\sqrt {4{b^2} - {a^2}} }}{2} \)\(= \frac{1}{4}a\sqrt {4{b^2} - {a^2}} .\)