Lý thuyết đường thẳng song song và đường thẳng cắt nhau

Lý thuyết đường thẳng song song và đường thẳng cắt nhau

Trong bài viết này Cunghocvui sẽ giới thiệu tới các bạn một nội dung học rất quan trọng và bổ ích về đường thẳng song song và đường thẳng cắt nhau luyện tập!

I. Lý thuyết

1. Đường thẳng song song 

Cho hai đường thẳng như sau: \(y=ax+b (a≠0) \ và \ y=a′x+b′ (a′≠0)\). Hai đường thẳng trên thỏa mãn điều kiện là hai đường song song khi đáp ứng các điều kiện sau: \(a=a′, \ b≠b′\). Đối với trường hợp đặc biệt là khi chúng trùng nhau, điều kiện thỏa mãn là: \(a=a′, \ b=b′\)

2. Đường thẳng cắt nhau

Cũng cho hai đường thẳng như trên, điều kiện để chúng có điểm giao nhau là khi hệ số góc của hai đường khác nhau, hay nói cách khác là a≠a′.

Bài tập hai đường song song

II. Bài tập vận dụng

Bài 1:

Cho hàm số \(y=2x+b.\) Tìm b ứng với từng yêu cầu cho trước như sau:

a) Đồ thì giao nhau với trục tung Oy tại điểm có tọa độ là (0; -3)

b) Điểm \(A(1; 5).\)thuộc đồ thị của hàm số trên.

Hướng dẫn:

- Đồ thị hàm số y = ax + b cắt trục tung tại điểm A(0; b).

- Điểm \(M( x_{M} ;  y_{M} )\) thuộc đồ thị hàm số \(y = ax + b <=>  y_{M} = a x_{M} + b.\)

Giải:

a) Đồ thị hàm số y = 2x + b cắt trục tung tại điểm có tung độ bằng -3 thì b = -3.

b) Thay x = 1, y = 5 vào hàm số y = 2x + b được:

5 = 2.1 + b <=> b = 3

Bài 2: Với hai hàm số như sau: \(y=2x+3k \ \ và \ y=(2m+1)x+2k−3.\)

Đối với các yêu cầu dưới đây thì điều kiện nào của m là thỏa mãn khi:

a) Chúng cắt nhau

b) Chúng song song

c) Chúng trùng nhau.

Hướng dẫn:

- y = ax + b được coi là bậc nhất nếu thỏa mãn điều kiện a ≠ 0.

- Với các tính chất và lý thuyết về vị trí tương đối của hai đường ta dễ dàng vận dụng như sau:

Hai đường thẳng: \(d: y = ax + b\) và \(d’: y = a'x + b’\)

d cắt d’ \(<=> a ≠ a’ \)

\(d // d’ <=> a = a’ \ và \ b ≠ b’\)

\(d ≡ d’ <=> a = a’ \ và \ b= b’\)

Giải:

a) \(y = (2m + l)x + 2k - 3\)  được coi là bậc nhất nếu thỏa mãn:

\(2m + l ≠ 0 <=> m ≠  \frac{-1}{2} \). Hai đường thẳng y = 2x + 3k và \(y = (2m + l)x + 2k - 3\) cắt nhau khi và chỉ khi: \(2m + I ≠ 2 <=> m ≠  \frac{1}{2}  \). Điều kiện của m là: \(m ≠  \frac{1}{2} \ và \ \frac{-1}{2} \)

b) \(y=2x+3k \ và \ y=(2m+1)x+2k−3.\) thỏa mãn tương quan song song khi:

\(m=\dfrac{1}{2} \ và \ k \neq -3\)

c) \(y=2x+3k \ và \ y=(2m+1)x+2k−3.\) thỏa mãn tương quan trùng nhau khi:

\(m=\dfrac{1}{2} \ và \ k = -3\)

Bài 3:

a) Trên mặt phẳng tọa độ, đồ thị của y và ý là:

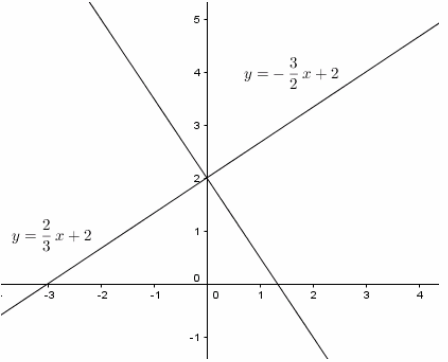
+) \(y=\dfrac{2}{3}x+2\)

+) \(y=-\dfrac{3}{2}x+2\)

b) Đầu bài ra như sau tìm phương trình của một đường thẳng bất kỳ cắt Oy tại điểm (0;1) và song song với trục Ox, khi đó đường đó đi qua các điểm giao của hai đường thẳng  \(y= \frac{2x}{3} +2 \ và \ y= \frac{-3x}{2} +2\)  và cắt đường thẳng thứ nhất tại M và cắt đường thẳng thứ hai tại N. Yêu cầu tìm vị trí tọa độ của hai điểm M và N?

Hướng dẫn:

- Theo giả thuyết cho đường thẳng song song với trục hoành. Bên cạnh đó cắt trục tung tại (0;1) chính vì vậy cần tìm b và phương trình có dạng y = b.

- Điểm giao của hai đường thẳng trên hội tụ tại một điểm: \(y = ax + b \ \ và \ y = a’x + b’\) là nghiệm của phương trình: \(ax + b = a’x + b’\)

Giải:

a) Theo đề bài  \(y =  \frac{2x}{3} + 2\) có  đồ thị cắt tại hai điểm \((0; 2) \ \ và \ (-3; 0).\)

Đường thảng của hàm số \(y =  \frac{-3x}{2} + 2\) cũng đi qua hai điểm giao \((0; 2) \ \ và \) \(( \frac{4}{3} ;0)\)

b) Theo giả thuyết cho đường thẳng song song với trục hoành. Bên cạnh đó cắt trục tung tại (0;1) chính vì vậy y = 1.

Đường y=1 và \(y =  \frac{2x}{3} + 2\) cắt nhau tại điểm M khi đó ta xác định được x và y của M là nghiệm của phương trình: \(\frac{2x}{3} + 2 = 1 <=> x =  \frac{-3}{2} \)

Vậy \(M( \frac{-3}{2} ; 1)\)

Đường y = 1 và đường thẳng \(y =  \frac{2x}{3} + 2\) cắt nhau tại giao điểm là N khi đó xác định được x và y của N là nghiệm của phương trình: \( \frac{-3x}{2} + 2 = 1 <=> x = \frac{2}{3} \)

Vậy: \(N( \frac{2}{3} ; 1)\)

Hy vọng rằng với những kiến thức mới về đường thẳng song song và đường thẳng cắt nhau lý thuyết trên đây, các bạn hoàn toàn có thể nắm chắc một cách dễ dàng và có những giờ học thư giãn!