Giải câu 9 Trang 80 - Sách giáo khoa Vật lí 12
a) \(Z_C=\dfrac{1}{C \omega}=\dfrac{1}{\dfrac{1}{4000\pi}.100\pi}=40(\Omega)\)
\(Z_L=L \omega=\dfrac{0,1}{\pi}.100\pi=10(\Omega)\)
\(Z=\sqrt{R^2+(Z_L-Z_C)^2}=\sqrt{40^2+(10-40)^2}=50(\Omega)\)
\(I_0=\dfrac{U_0}{Z}=\dfrac{120\sqrt{2}}{50}=2,4\sqrt{2}(A)\)
Độ lệch pha giữa u và i là \(\varphi\).
Ta có: \(\tan \varphi=\dfrac{Z_L-Z_C}{R}=\dfrac{10-40}{40}=-\dfrac{3}{4}\)
\(\Rightarrow \varphi =-\dfrac{37\pi}{180}(rad)\)
Biểu thức tức thời của cường độ dòng điện:
\(i=2,4\sqrt{2} \cos \left ( 100\pi t+\dfrac{37\pi}{180}\right )(A)\)
b)
* Điện áp hiệu dụng ở hai đầu AM:
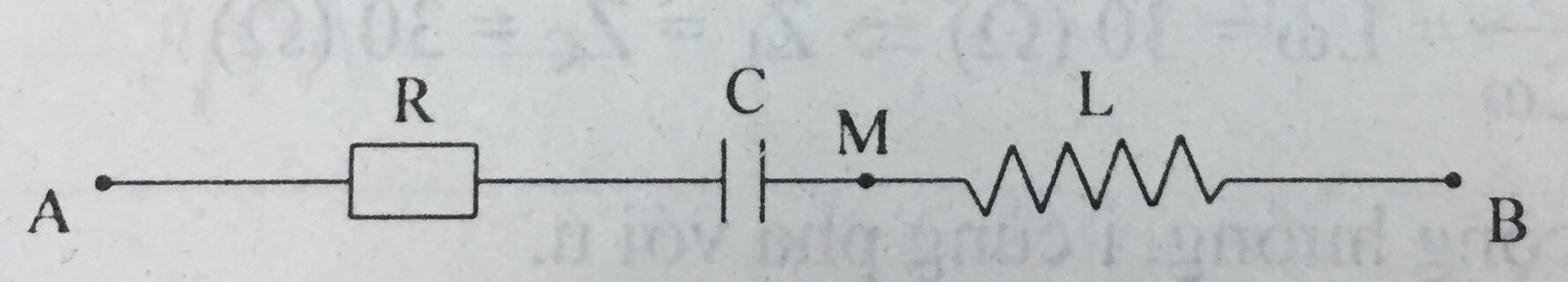
\(I=\dfrac{I_0}{\sqrt{2}}=\dfrac{2,4\sqrt{2}}{\sqrt{2}}=2,4(A)\)
\(U_R=IR=2,4.40=96(V)\)
\(U_C=IZ_C=2,4.40=96(V)\)
\(U_{AM}=\sqrt{U_R^2+U_C^2}=96\sqrt{2}(V)\)
Vậy, điện áp hiệu dụng ở hai đầu AM bằng \(96\sqrt{2}(V).\)

