Tổng hợp đầy đủ lý thuyết cần nhớ về góc nội tiếp bộ môn Toán 9

Trong Toán hình học lớp 9, các em học sinh sẽ được học về góc nội tiếp. Đây là phần kiến thức quan trọng để làm nhiều bài tập hình học khác. Bài viết dưới đây sẽ tổng hợp lý thuyết về chủ đề này. 

1. Định nghĩa 

- Góc có đỉnh nằm trên đường tròn, hai cạnh chứa hai dây cung đường tròn đó gọi là góc nội tiếp. 

- Cung nằm bên trong góc nội tiếp là cung bị chắn.

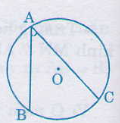
Ví dụ: Góc nội tiếp \(\widehat{BAC}\) và cung bị chắn BC. 

 

2. Định lý 

Trong đường tròn, số đo góc nội tiếp bằng một nửa số đo cung bị chắn. 

Chứng minh định lý: Trường hợp tâm O đường tròn nằm trong góc \(\widehat{BAC}\) 

Vì tâm O đường tròn nằm trong góc \(\widehat{BAC}\) nên tia AD nằm giữa hai tia AB, AC. 

Có: \(\widehat{BAC}\) = \(\widehat{BAD} + \widehat{DAC}\)

Số đo cung bị chắn BC = Số đo cung bị chắn DC + số đo cung bị chắn BD. 

Mà \(\widehat{BAD} = \dfrac{1}{2} \) số đo cung bị chắn BD; \(\widehat{DAC} = \dfrac{1}{2} \)số đo cung bị chắn DC. 

=> \(\widehat{BAC}\) = \(\dfrac{1}{2} \)(số đo cung bị chắn BD + số đo cung bị chắn DC). 

Vậy \(\widehat{BAC}\) = \(\dfrac{1}{2} \) số đo cung bị chắn BC. 

Nếu O nằm trên một cạnh của góc \(\widehat{BAC}\) hoặc nằm ngoài góc \(\widehat{BAC}\) cũng chứng minh tương tự. 

3. Tính chất

- Góc nội tiếp bằng nhau thì chắn các cung bằng nhau.

- Góc nội tiếp chắn một cung hay các cung bằng nhau sẽ bằng nhau. 

- Góc nội tiếp có số đo bằng nửa số đo góc ở tâm thì cùng chắn một cung. 

- Góc nội tiếp chắn nửa đường tròn là góc có 90\(^o\).

Trên đây là toàn bộ lý thuyết về góc nội tiếp, rất mong bổ ích đối với độc giả! Sau khi học xong, độc giả có thể tham khảo cách giải bài tập góc nội tiếp tại cunghocvui.com.