Đề kiểm tra 15 phút - Đề số 5 - Bài 2 - Chương 1 - Hình học 7

Đề bài

Lấy điểm O thuộc đường thẳng xy. Trên nửa mặt phẳng bờ là đường thẳng xy, vẽ hai tia Om và On sao cho \(\widehat {nOm'}.\) \(\widehat {xOm} = \widehat {yOn} = {120^o}\). Gọi Om’ là tia đối của tia Om.

a) Chứng minh \(\widehat {xOn} = \widehat {xOm'}.\)

b) Chứng minh rằng tia Ox là tia phân giác của góc nOm’.

Hướng dẫn giải

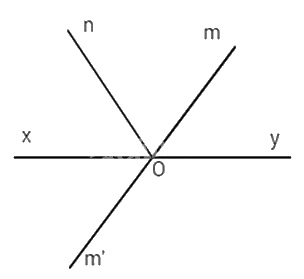
a) Ta có  \(\widehat {xOm} + \widehat {mOy} = {180^o}\) (vì Ox và Oy là hai tia đối nhau)

\( \Rightarrow \widehat {mOy} = {180^o} - \widehat {xOm}\)

\(\;\;\;\;\;\;\;\;\;\;\;\;\;\,={180^o} - {120^o} = {60^o}.\)

Tương tự ta có \(\widehat {xOn} = \widehat {mOy} = {60^o}\)

Mà \(\widehat {xOm'} = \widehat {yOm} = {60^o}\) (đối đỉnh)

\( \Rightarrow \widehat {xOn} = \widehat {xOm'} = {60^o}.\)

b) Ta có \( \Rightarrow \widehat {mOn} <\widehat {mox} <\widehat {mom'}\,\)\(\left( {{{60}^o} <{{120}^o} <{{180}^o}} \right).\)

Do đó Ox nằm giữa hai tia On và Om’ và \( \widehat {xOn} = \widehat {xOm'} = {60^o}.\) Chứng tỏ Ox là tia phân giác của \(\widehat {nOm'}.\)