Đề kiểm tra 15 phút - Đề số 2 - Bài 1 - Chương 2 - Hình học 7

Đề bài

Trên đường thẳng xx’ lấy một điểm O. Trên nửa mặt phẳng bờ xx’ vẽ tia Oy sao cho $\widehat {x'Oy'}$ $\widehat {xOy} = {45^o}.$ Trên nửa mặt phẳng kia vẽ tia Oz sao cho $Oz \bot O$ x. Gọi Oy’ là tia phân giác của $\widehat {x'Oz}.$

a) Chứng minh $\widehat {xOy}$ và $\widehat {x'Oy'}$ là hai góc đối đỉnh.

b) Trên nửa mặt phẳng bờ xx’ có chứa tia Oy vẽ tia Ot sao cho $Ot \bot Oy.$ Hãy tính $\widehat {x'Ot}.$

Hướng dẫn giải

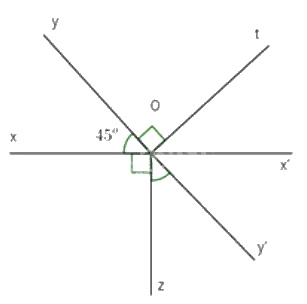
a) Ox’ và Ox là hai tia đối nhau nên $\widehat {xOx'} = {180^o}$ mà $\widehat {xOz} = {90^o} \Rightarrow \widehat {x'Oz} = {90^o}.$

Mặt khác Oy là tia phân giác của $\widehat {x'Oz}$ nên$\widehat {x'Oy'} = \widehat {zOy'} = {1 \over 2}{.90^o} = {45^o}$

$\Rightarrow \widehat {x'Oy'} = \widehat {xOy} = {45^o}$ mà Ox’ và Ox là hai tia đối nhau, hai tia Oy’ và Oy thuộc hai mặt phẳng đối nhau có bờ là xx’. Do đó $\Rightarrow \widehat {x'Oy'}$ và $\widehat {xOy}$ là hai góc đối đỉnh.

b) Ta có Oy’ và Oy là hai tia đối nhau ( chứng minh trên)

$\widehat {AOC} = {60^o}.$ $\Rightarrow \widehat {yOt} + \widehat {tOy'} = {180^o}$ hay ${90^o} + \widehat {tOy'} = {180^o}$$\Rightarrow \widehat {tOy'} = {90^o}.$ Lại có Oy’ và Oy thuộc hai nửa mặt phẳng đối nhau bờ xx’ nên Ox’ nằm giữa hai tia Oy và Oy’. Do đó $\widehat {tOx'} + \widehat {x'Oy'} = \widehat {tOy'}$ hay $\widehat {tOx'} + {45^o} = {90^o} \Rightarrow \widehat {tOx'} = {45^o}.$