Đề kiểm tra 15 phút - Đề số 2 - Bài 1 - Chương 2 - Hình học 7 (tập 1)
Đề bài
Cho tam giác ABC có \(\widehat {BIC} > \widehat {BAC}.\) \(\widehat A = {80^o}\),tia phân gisc của góc B và C cắt nhau tại I. Gọi D là giao điểm của AI với BC.
a) Tính số đo của góc \(\widehat {BIC}\)
b) So sánh \(\widehat {BID}\) và \(\widehat {BAD}\); \(\widehat {BIC}\) và \(\widehat {BAC}\).
Hướng dẫn giải
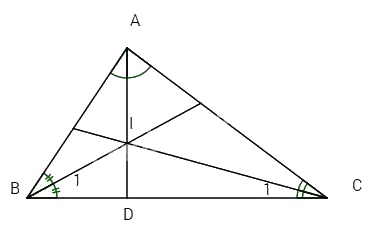
a) Ta có \(\widehat A + \widehat B + \widehat C = {180^0}\)
\( \Rightarrow \widehat B + \widehat C = {180^0} - \widehat A = {100^o}.\)
\( \Rightarrow\dfrac {{\widehat B + \widehat C}}{ 2} = {50^o} \Rightarrow \widehat {{B_1}} + \widehat {{C_1}} = {50^o}\)
Xét ta có
\(\widehat {BIC} = {180^o} - \left( {\widehat {{B_1}} + \widehat {{C_1}}} \right)\)
\(\eqalign{\;\;\;\;\;\;\; & = {180^o} - 50 \cr & = {130^o}. \cr} \)
b) Ta có \(\widehat {BID}\) là góc ngoài của nên \(\widehat {BID} > \widehat {BAD}.\)
Chứng minh tương tự ta có \(\widehat {CID} > \widehat {CAD}.\)
Do đó: \(\widehat {BID} + \widehat {CID} > \widehat {BAD} + \widehat {CAD}\) hay \(\widehat {BIC} > \widehat {BAC}.\)

