Bài 5 trang 69 SGK Toán 9 tập 2

Đề bài

 Hai tiếp tuyến của đường tròn \((O)\) tại \(A\) và \(B\) cắt nhau tại \(M\). Biết \(\widehat{AMB}\).

a) Tính số đo của góc ở tâm tạo bởi hai bán kính \(OA, OB\).

b) Tính số đo mỗi cung \(AB\) (cung lớn và cug nhỏ).

Hướng dẫn giải

Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.

Số đo của cung lớn bằng hiệu giữa \({360^o}\) và số đo của cung nhỏ (có chung hai mút với cung lớn)

Số đo của nửa đường tròn bằng \({180^o}\)

Lời giải chi tiết

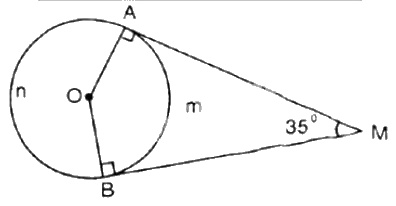
a) Trong tứ giác \(AOBM\) có \(\widehat A = \widehat B = {90^0}\)

Suy ra: \(\widehat {AOB} + \widehat {AMB} = {180^0}\)

\(\widehat {AOB} = {180^0} - {35^0} = {145^0}\)

b) Từ \(\widehat {AOB} = {145^0}\). Suy ra số đo cung nhỏ \(\overparen{AB}\) là \(145^0\)và số đo cung lớn \(\overparen{AB}\) : \({360^0} - {145^0} = {215^0}\)