Bài 38 trang 62 SGK Toán 9 tập 1

Đề bài

a) Vẽ đồ thị các hàm số sau trên cùng một mặt phẳng tọa độ:

y = 2x (1);

y = 0,5x (2);

y = -x + 6 (3)

b) Gọi các giao điểm của đường thẳng có phương trình (3) với hai đường thẳng có phương trình (1) và (2) theo thứ tự là A và B. Tìm tọa độ của hai điểm A và B.

c) Tính các góc của tam giác OAB.

Hướng dẫn câu c)

Tính OA, OB rồi chứng tỏ tam giác OAB là tam giác cân.

Tính \(\widehat {AOB} = \widehat {AOx} - \widehat {BOx}\)

Hướng dẫn giải

+) Muốn tìm tọa độ giao điểm của 2 đường thẳng y = ax + b và y = a'x + b' thì ta viết phương trình hoành độ giao điểm của 2 đt: ax + b = a'x + b' sau đó ta tìm được x, thay x vào 1 trong 2 phương trình đường thẳng ta tìm được y. Từ đó tìm được tọa độ giao điểm của 2 đường thẳng.

+) Sử dụng hệ thức lượng trong tam giác vuông để tìm góc liên quan đến các góc trong tam giác cần tìm.

Lời giải chi tiết

a) Đồ thị xem hình dưới

Đồ thị hàm số y = 2x đi qua điểm (1;2) và (2;4)

Đồ thị hàm số y = 0,5 x  đi qua điểm (2;1) và (4;2)

Đồ thị hàm số y =  - x + 6  đi qua điểm (0;6) và (6;0)

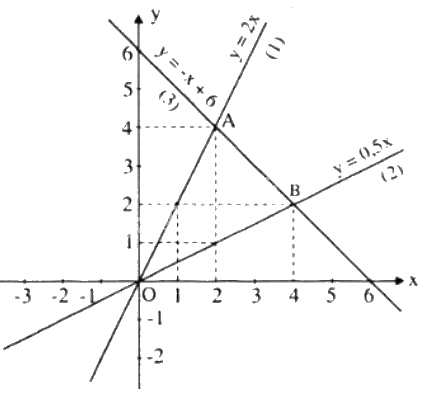
b) Tìm tọa độ điểm A.

Phương trình hoành độ giao điểm của (1) và (3) là:

-x + 6 = 2x ⇔ 6 = 2x + x ⇔ x = 2

x = 2 thì y = -2 + 6 = 4 nên A(2; 4)

Tìm tọa độ điểm B.

Phương trình hoành độ giao điểm của (2) và (3) là:

-x + 6 = 0,5x ⇔ 6 = 0,5x + x ⇔ x = 4

Với x = 4 thì y = -4 + 6 = 2 nên B(4;2)

c)  

\(\eqalign{
& O{A^2} = {2^2} + {4^2} = 20 \Rightarrow OA = \sqrt {20} \cr
& O{B^2} = {4^2} + {2^2} = 20 \Rightarrow OB = \sqrt {20} \cr
& OA = OB\left( { = \sqrt {20} } \right) \cr} \)

⇒ ∆OAB cân tại O

Ta có \(tg\widehat {BOx} = {2 \over 4} = {1 \over 2} \Rightarrow \widehat {BOx} \approx {26^0}34'\)

và  \(tg\widehat {AOx} = {4 \over 2} = 2 \Rightarrow \widehat {AOx} \approx {63^0}26'\)

Do đó \(\widehat {AOB} = \widehat {AOx} - \widehat {BOx} = {36^0}52'\)

Nên \(\widehat {OAB} = \widehat {OBA} \approx {{{{180}^0} - {{36}^0}52'} \over 2} = {71^0}34'\)