Bài 3 trang 91 SGK Hình học 11

Đề bài

Cho hình bình hành \(ABCD\). Gọi \(S\) là một điểm nằm ngoài mặt phẳng chứa hình bình hành. chứng minh rằng: \(\overrightarrow{SA}\) + \(\overrightarrow{SC}\) = \(\overrightarrow{SB}\) + \(\overrightarrow{SD}\).

Hướng dẫn giải

Sử dụng công thức: \(\overrightarrow {MA}  + \overrightarrow {MB}  = 2\overrightarrow {MI} \), với \(M\) là một điểm nằm ngoài \(AB\) và \(I\) là trung điểm của \(AB\).

Lời giải chi tiết

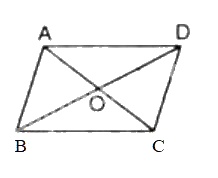
Gọi \(O\) là tâm của hình bình hành \(ABCD\), ta có \(O\) là trung điểm của \(AC\) và \(BD\). Khi đó: 

\(\left\{ \matrix{\overrightarrow {SA} + \overrightarrow {SC} = 2\overrightarrow {SO} \hfill \cr \overrightarrow {SB} + \overrightarrow {SD} = 2\overrightarrow {SO} \hfill \cr} \right.\)\( \Rightarrow\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD}\,\,\left( {dpcm} \right)\)