Bài 19 trang 52 SGK Toán 9 tập 1
Đề bài
Đồ thị của hàm số \(y = \sqrt 3 x + \sqrt 3 \) được vẽ bằng compa và thước thẳng.
Hãy tìm hiểu cách vẽ đó rồi nêu lại các bước thực hiện.
Áp dụng: Vẽ đồ thị của hàm số \(y = \sqrt 5 x + \sqrt 5 \) bằng compa và thước thẳng.
Hướng dẫn. Tìm điểm trên trục tung có tung độ bằng \(\sqrt 5 \).
Hướng dẫn giải
+) Xác định hai điểm thuộc đồ thị hàm số \(y=ax+b(a \ne 0)\):
Cho \(x=0 \Rightarrow y=b \Rightarrow A(0; b).\)
Cho \(y=0 \Rightarrow x = -\dfrac{b}{a} \Rightarrow B {\left(-\dfrac{b}{a} \right)}.\)
Xác định vị trí hai điểm \(A,\ B\) trên mặt phẳng tọa độ. Đường thẳng đi qua \(A,\ B\) là đồ thị hàm số \(y=ax+b\)
+) Định lí Py-ta-go trong tam giác vuông: Cho tam giác \(ABC\) vuông tại \(A\). Khi đó:
\(BC^2=AB^2+AC^2\).
Lời giải chi tiết
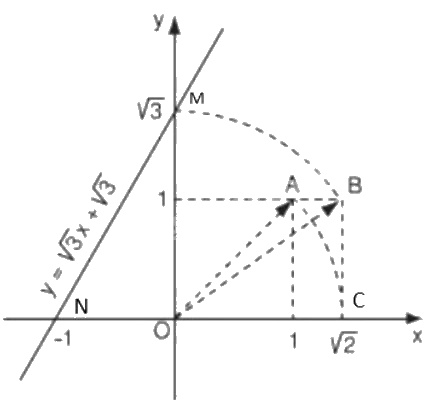
+ Vẽ đồ thì hàm số: \(y=\sqrt 3 x + \sqrt 3\)
Cho \(x= 0 \Rightarrow y = \sqrt 3 . 0 + \sqrt 3 = \sqrt 3 \Rightarrow M(0; \sqrt 3)\).
Cho \(y=0 \Rightarrow 0 = \sqrt 3 . x + \sqrt 3 \Rightarrow x= -1 \Rightarrow N(-1; 0)\).
Đồ thị hàm số \(y=\sqrt 3 x + \sqrt 3\) là đường thẳng đi qua hai điểm \(M(0; \sqrt 3)\) và \(N(-1; 0)\)
+ Ta đi xác định vị trí điểm \(M(0; \sqrt 3)\) trên trục tung:
Bước \(1\): Xác định điểm \(A(1; 1)\) trên mặt phẳng tọa độ \(Oxy\). Khi đó theo định lí Py-ta-go, ta có:
\(OA^2=1^2+1^2=2 \Leftrightarrow OA =\sqrt 2\)
Bước \(2\): Dùng compa vẽ cung tròn tâm \(O\) bán kính \(OA =\sqrt 2\). Cung tròn này cắt trục \(Ox\) tại vị trí \(C\) thì hoành độ của \(C\) là \(\sqrt 2\).
Bước \(3\): Xác định điểm \(B( \sqrt 2; 1)\). Khi đó theo định lí Py-ta-go, ta có:
\(OB^2=(\sqrt 2)^2+1^2=2=1=3 \Leftrightarrow OB =\sqrt 3\)
Bước \(4\): Dùng compa vẽ cung tròn tâm \(O\) bán kính \(OB=\sqrt 3\). Khi đó cung tròn này cắt trục tung tại vị trí điểm có tung độ là \(\sqrt 3\). Ta xác định được điểm \(M(0; \sqrt 3)\).
Bước \(5\): Kẻ đường thẳng đi qua hai điểm \(M\) và \(N\) ta được đồ thị hàm số \(y=\sqrt 3 x + \sqrt 3\).
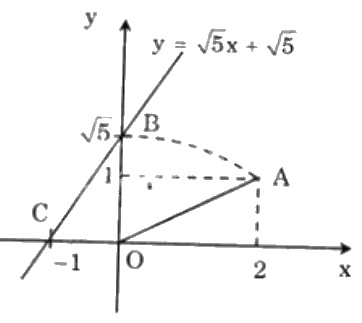
+ Áp dụng: Vẽ đồ thị hàm số \(y = \sqrt 5 x + \sqrt 5 \) (làm tương tự như trên)
Cho \(x= 0 \Rightarrow y = \sqrt 5 . 0 + \sqrt 5 = \sqrt 5 \Rightarrow B(0; \sqrt 5)\).
Cho \(x= -1 \Rightarrow y = \sqrt 5 . (-1) + \sqrt 5 = 0 \Rightarrow C(-1; 0)\).
Bước \(1\): Xác định điểm \(A(2; 1)\) trên mặt phẳng tọa độ \(Oxy\).
Áp dụng định lí Py-ta-go, ta có:
\(OA^2=2^2+1^2=4+1=5 \Leftrightarrow OA = \sqrt 5\)
Bước \(2\): Vẽ cung tròn tâm \(O\) bán kính \(OA=\sqrt 5\). Cung tròn này cắt trục \(Oy\) tại vị trí điểm \(B\) có tung độ là \(\sqrt 5\). Ta xác định được điểm \(B\).
Bước \(3\): Kẻ đường thẳng đi qua hai điểm \(B(0; \sqrt 5)\) và \(C(-1; 0)\) ta được đồ thị của hàm số \(y = \sqrt 5 x + \sqrt 5 \).