Giải bài 19 trang 52 - Sách giáo khoa Toán 9 tập 1

Đề bài

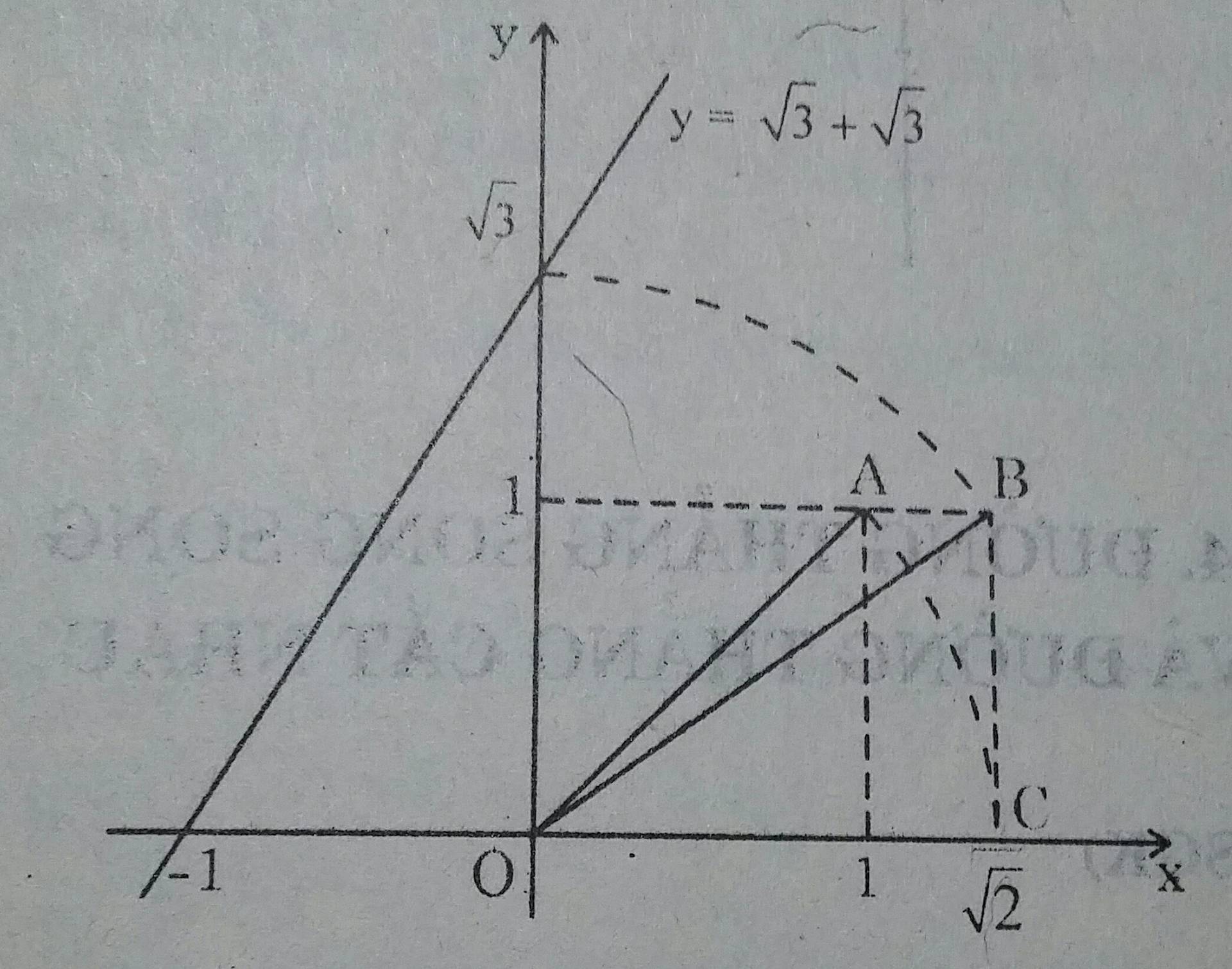
   Đồ thị của hàm số    \(y =\sqrt{3}x + \sqrt{3}\) được vẽ bằng compa và thước thẳng (h.8). 

 Hãy thực hiện cách vẽ đó rồi nêu lại cách thực hiện.

 Áp dụng: Vẽ đồ thị của hàm số  \(y =\sqrt{3}x+ \sqrt{3}\) bằng compa và thước thẳng.

 

Hướng dẫn giải

      Hướng dẫn: 

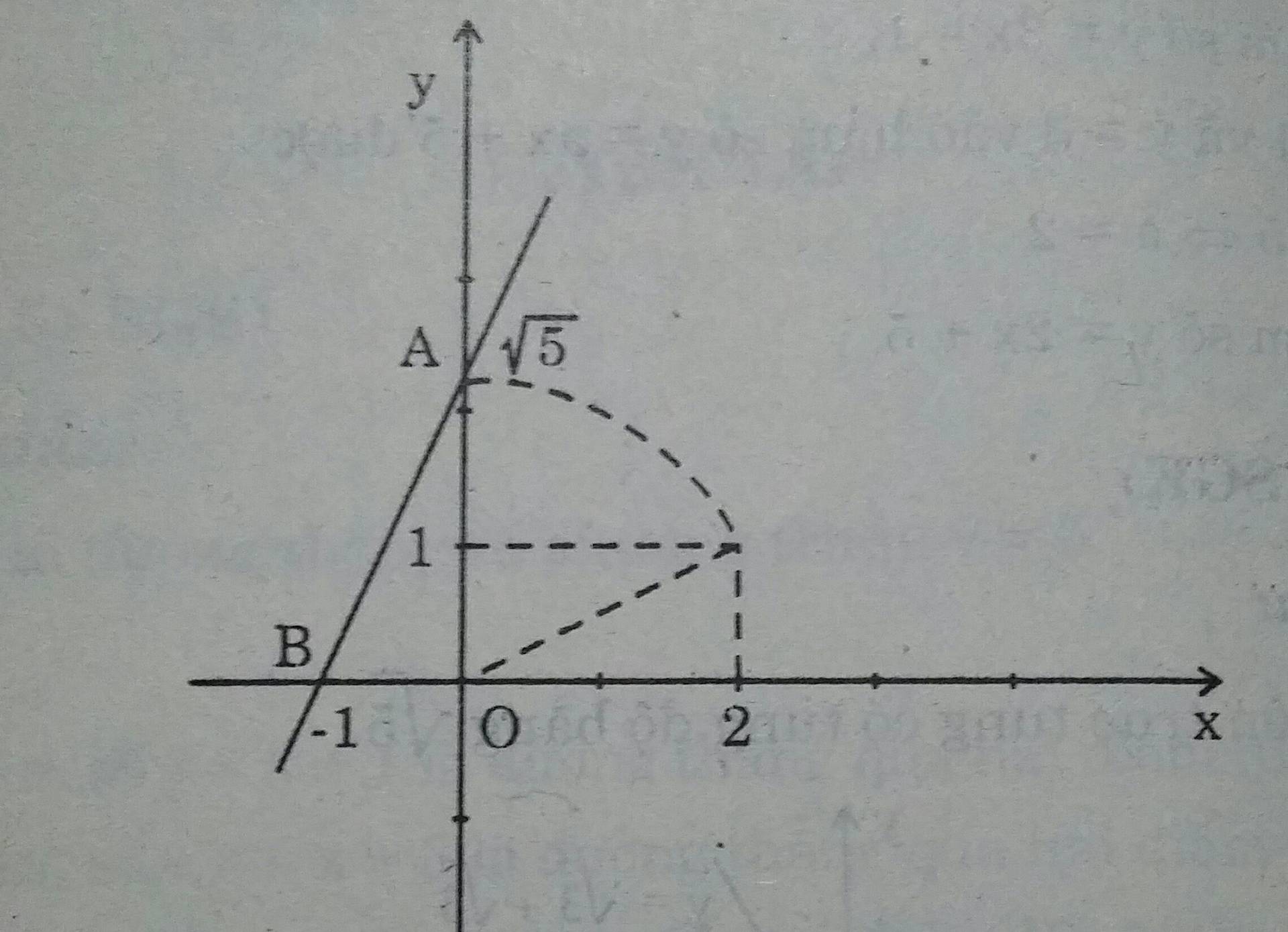
   Tìm điểm trên trục tung có tung độ bằng \( \sqrt{5}\)

      Giải: 

    Gọi A(1;1) thì \( OA= \sqrt{1^2+ 1^2}= \sqrt{2}\)

    Lấy điểm C trên Ox có tọa độ \(C( \sqrt{2}; 0) \) và gọi \(B( \sqrt{2};1)\)

   Khi đó \(OB= \sqrt{( \sqrt{2})^2+1^2}= \sqrt{3}\). Dũng compa dựng \(D(0; \sqrt{3})\)

   Đồ thị hàm số \(y = \sqrt{3}x + \sqrt{3}\)  là đường thẳng đi qua hai điểm \(D( 0; \sqrt{3}) \) và \( E( -1; 0) \)

  Vẽ đồ thị hàm số \(y = \sqrt{5}x + \sqrt{5}\) 

   Với x=0 thì \(y = ​​\sqrt{5}\); với y =0 thì x= -1. Đồ thị hàm số là đường thẳng đi qua hai điểm \(A( 0; \sqrt{5})\) và B( -1; 0) 

   Cách dựng đoạn thẳng có độ dài bằng \(\sqrt{5}\) như hình vẽ.