40 bài tập trắc nghiệm giá trị lớn nhất, giá trị n...
- Câu 1 : Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) sao cho \(\mathop {\max }\limits_{\left[ { - 1;4} \right]} f\left( x \right) = 3\). Đặt \(g\left( x \right) = f\left( {3{x^3} + 2x - 1} \right) + 2m\), \(m\) là tham số. Tìm \(m\) để \(\mathop {\max }\limits_{\left[ {0;1} \right]} g\left( x \right) = - 7\).
A \(m = 7\)
B \(m = - 2\)
C \(m = 2\)
D \(m = - 5\)
- Câu 2 : Cho hàm số \(y = f\left( x \right)\), hàm số \(y = f'\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ sau
A \(m \ge f\left( 2 \right) - 2\).
B \(m \le f\left( 0 \right)\).
C \(m > f\left( 2 \right) - 2\).
D \(m < f\left( 0 \right)\).
- Câu 3 : Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên đoạn \(\left[ {0;\dfrac{7}{2}} \right]\) có đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ. Hỏi hàm số \(y = f\left( x \right)\)đạt giá trị nhỏ nhất trên đoạn \(\left[ {0;\dfrac{7}{2}} \right]\) tại điểm \({x_0}\) nào dưới đây?
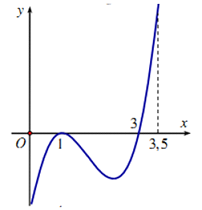
A \({x_0} = - 1\)
B \({x_0} = 0\)
C \({x_0} = 1\)
D \({x_0} = 3\)
- Câu 4 : Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên. Xét hàm số \(g\left( x \right) = f\left( {{x^3} + 2x} \right) + m\). Giá trị của tham số \(m\) để giá trị lớn nhất của hàm số \(g\left( x \right)\) trên đoạn \(\left[ {0;1} \right]\) bằng \(9\) là:
A \(m = 10\)
B \(m = 6\)
C \(m = 12\)
D \(m = 8\)
- Câu 5 : Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị \(y = f'\left( x \right)\) như hình vẽ. Đặt \(g\left( x \right) = 2f\left( x \right) - {x^2}\). Khi đó giá trị lớn nhất của hàm số \(g\left( x \right)\) trên đoạn \(\left[ { - 2;4} \right]\) là:
A \(g\left( { - 2} \right)\).
B \(g\left( 2 \right)\).
C \(g\left( 4 \right)\).
D \(g\left( 0 \right)\).
- Câu 6 : Cho hàm số \(f\left( x \right) = \left| {3{x^4} - 4{x^3} - 12{x^2} + m} \right|\). Gọi \(M\) là giá trị lớn nhất của hàm số trên đoạn \(\left[ { - 1;3} \right]\). Tổng các giá trị của tham số thực \(m\) để \(M = \dfrac{{71}}{2}.\)
A \(4\)
B \(- 3\)
C \(9\)
D \(5\)
- Câu 7 : Một sợi dây kim loại dài \(a\,\,\left( {{\rm{cm}}} \right)\) . Người ta cắt sợi dây đó thành hai đoạn, trong đó một đoạn có độ dài \(x\,\,\left( {{\rm{cm}}} \right)\) được uốn thành đường tròn và đoạn còn lại được uốn thành hình vuông \(\left( {a > x > 0} \right).\) Tìm \(x\) để hình vuông và hình tròn tương ứng có tổng diện tích nhỏ nhất.
A \(x = \dfrac{a}{{\pi + 4}}\left( {{\rm{cm}}} \right)\)
B \(x = \dfrac{{2a}}{{\pi + 4}}\left( {{\rm{cm}}} \right)\)
C \(x = \dfrac{{\pi a}}{{\pi + 4}}\left( {{\rm{cm}}} \right)\)
D \(x = \dfrac{{4a}}{{\pi + 4}}\left( {{\rm{cm}}} \right)\)
- Câu 8 : Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 1;4} \right]\) và có đồ thị như hình vẽ
A \(6\)
B \(5\)
C \(7\)
D \(8\)
- Câu 9 : Tìm giá trị nhỏ nhất của hàm số \(y = x + \dfrac{{16}}{{\sqrt x }}.\)
A \(8\)
B \(3\sqrt 8 \)
C \(16\)
D \(12\)
- Câu 10 : Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình dưới. Gọi \(a,\,\,A\) lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của \(f\left( {x + 1} \right)\) trên đoạn \(\left[ { - 1;\,\,0} \right].\) Giá trị \(a + A\) bằng:
A \(1\)
B \(2\)
C \(0\)
D \(3\)
- Câu 11 : Cho hàm số \(f\left( x \right)\). Biết hàm số \(f'\left( x \right)\) có đồ thị như hình dưới đây. Trên đoạn \(\left[ { - 4;3} \right]\), hàm số \(g\left( x \right) = 2f\left( x \right) + {\left( {1 - x} \right)^2}\) đạt giá trị nhỏ nhất tại điểm
A \(x = - 1\).
B \(x = - 4\).
C \(x = - 3\).
D \(x = 3\).
- Câu 12 : Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên. Gọi \(k,\,\,K\) lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y = f\left( { - 2x} \right)\) trên đoạn \(\left[ { - 1;\,\,\dfrac{1}{2}} \right].\)Giá trị của \(k + K\) bằng:
A \(4\)
B \(0\)
C \(\dfrac{{19}}{8}\)
D \( - 4\)
- Câu 13 : Cho hàm số \(y = f\left( x \right)\) có đạo hàm là \(f'\left( x \right)\). Đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ bên. Biết rằng \(f\left( 0 \right) + f\left( 3 \right) = f\left( 2 \right) + f\left( 5 \right)\). Giá trị nhỏ nhất, giá trị lớn nhất của \(f\left( x \right)\) trên \(\left[ {0;5} \right]\) lần lượt là:
A \(f\left( 0 \right);f\left( 5 \right)\)
B \(f\left( 2 \right);f\left( 0 \right)\)
C \(f\left( 2 \right);f\left( 5 \right)\)
D \(f\left( 1 \right);f\left( 5 \right)\)
- Câu 14 : Cho hàm số\(y = {x^3} + \left( {{m^2} + 1} \right)x + {m^2} - 2\) . Tìm số thực dương m để hàm số có giá trị nhỏ nhất trên đoạn \(\left[ {0;2} \right]\) bằng 2.
A \(m = {\rm{ }}2.\)
B \(m = {\rm{ }}4.\)
C \(m = 1.\)
D \(m = {\rm{ }}0.\)
- Câu 15 : Một chất điểm chuyển động có phương trình \({\rm{S}}\left( t \right) = - \dfrac{1}{3}{t^3} + 6{t^2}\) với thời gian t tính bằng giây (s) và quãng đường S tính bằng mét (m). Trong thời gian 5 giây kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của chất điểm đạt được là
A \(35m/s\)
B \(36m/s\)
C \(288m/s\)
D \(\dfrac{{325}}{3}m/s\)
- Câu 16 : Cho hàm số \(y = f\left( x \right) = a{x^4} + b{x^2} + c\left( {a \ne 0} \right)\) có \(\mathop {\min }\limits_{\left( { - \infty ;0} \right)} f\left( x \right) = f\left( { - 1} \right).\) Giá trị nhỏ nhất của hàm số trên \(\left[ {0;2} \right]\) bằng ?
A \(c\)
B \(c - a\)
C \(c + 8a\)
D \(16a + 4b + c\)
- Câu 17 : Một doanh nghiệp sản xuất và bán một loại sản phẩm với giá 45 (ngàn đồng) mỗi sản phẩm, tại giá bán này khách hàng sẽ mua 60 sản phẩm mỗi tháng. Doanh nghiệp dự định tăng giá bạn và họ ước tính rằng nếu tăng 2 (ngàn đồng) trong giá bán thì mỗi tháng sẽ bán ít hơn 6 sản phẩm. Biết rằng chi phí sản xuất mỗi sản phẩm là 27 (ngàn đồng). Hỏi doanh nghiệp nên bán sản phẩm với giá nào để lợi nhuận thu được lớn nhất?
A 47 ngàn đồng
B 46 ngàn đồng
C 48 ngàn đồng
D 49 ngàn đồng
- Câu 18 : Một bác nông dân cần xây một hố ga không có nắp dạng hình hộp chữ nhật có thể tích \(25600\left( {c{m^3}} \right)\), tỉ số giữa chiều cao của hố và chiều rộng của đáy bằng \(2\). Tính diện tích của đáy hố ga để khi xây hố ga tiết kiệm nguyên vật liệu nhất.
A \(640\left( {c{m^2}} \right)\)
B \(1600\left( {c{m^2}} \right)\)
C \(160\left( {c{m^2}} \right)\)
D \(6400\left( {c{m^2}} \right)\)
- Câu 19 : Tìm diện tích lớn nhất của hình chữ nhật nội tiếp trong nửa đường tròn bán kính 10cm, biết một cạnh của hình chữ nhật nằm dọc trên đường kính của đường tròn.
A 80\(c{m^2}\).
B 100\(c{m^2}\).
C 160\(c{m^2}\).
D 200\(c{m^2}\).
- Câu 20 : Cho hàm số \(y = \sqrt {4 + x} + \sqrt {4 - x} .\) Khằng định nào sau đây là đúng ?
A Giá trị lớn nhất của hàm số bằng \(4.\)
B Hàm số đạt giá trị nhỏ nhất tại \(x = 0\).
C Hàm số đạt giá trị lớn nhất tại \(x = 4\).
D Giá trị lớn nhất của hàm số bằng \(4.\)
- Câu 21 : Giá trị nhỏ nhất của hàm số \(f\left( x \right) = \frac{{{x^2} - x + 1}}{{x - 1}}\) trên khoảng \(\left( {1; + \infty } \right)\) là
A \(\mathop {\min }\limits_{\left( {1; + \infty } \right)} y = 3.\)
B \(\mathop {\min }\limits_{\left( {1; + \infty } \right)} y = - 1.\)
C \(\mathop {\min }\limits_{\left( {1; + \infty } \right)} y = 5.\)
D \(\mathop {\min }\limits_{\left( {1; + \infty } \right)} y = \frac{{ - 7}}{3}.\)
- Câu 22 : Diện tích lớn nhất của hình chữ nhật \(ABCD\) nội tiếp trong nửa đường tròn (tham khảo hình vẽ) có bán kính bằng \(10\,\,cm\) là:
A \(100 \,\,c{m^2}.\)
B \(160 \,\,c{m^2}.\)
C \(80 \,\,c{m^2}.\)
D \(200 \,\,c{m^2}.\)
- Câu 23 : Xét hàm số \(f\left( x \right) = {x^4} + a{x^3} + b{x^2} + cx + 1\) với \(a,\,\,b,\,\,c\) là các số thực không âm. Giả sử phương trình \(f\left( x \right) = 0\) có 4 nghiệm phân biệt. Tìm giá trị nhỏ nhất của biểu thức \(P = a + \dfrac{b}{2} + \dfrac{c}{4}\).
A \(7\)
B \(\dfrac{7}{2}\)
C \(8\)
D \(10\)
- Câu 24 : Bố và hai con trai đi từ nhà ra công viên cách nhà 16,8km. Bố có một xe máy, nhưng chỉ chở thêm được một người nữa. Biết rằng vận tốc xe máy là 24km/h, vận tốc đi bộ là 6km/h. Hỏi thời gian ngắn nhất để cả 3 bố con đến được công viên là bao nhiêu lâu, biết rằng họ khởi hành từ nhà cùng một lúc.
A 1 giờ 10 phút.
B 1 giờ 24 phút.
C 1 giờ 12 phút.
D 1 giờ 18 phút.
- Câu 25 : Cho hàm số \(y = f\left( x \right) = m{x^4} + 2{x^2} - 1\) với \(m\) là tham số thực. Có tất cả bao nhiêu giá trị nguyên của \(m\) thuộc khoảng \(\left( { - 2019;2020} \right)\) sao cho hàm số đã cho đồng biến trên khoảng \(\left( {0;\frac{1}{2}} \right)\)?
A \(4\)
B \(2016\)
C \(2024\)
D \(4037\)
- Câu 26 : Một thừa đất hình chữ nhật có chiều dài bằng \(20\) mét và chiều rộng bằng \(10\) mét, người ta giảm chiều dài \(x\) mét (với \(0 < x < 20\) ) và tăng chiều rộng thêm \(2x\) mét để được thửa đất mới. Tìm \(x\) để thửa đất mới có diện tích lớn nhất?
A \(x = \dfrac{{15}}{2}\)
B \(x = \dfrac{{15}}{4}\)
C \(x = 10\)
D \(x = 15\)
- Câu 27 : Giả sử \(m\) là số thực để giá trị lớn nhất của hàm số \(y = \left| {2{x^2} - 3x + 4m + 5} \right|\) trên đoạn \(\left[ { - 1;2} \right]\) là nhỏ nhất và \(m = \dfrac{a}{b}\) với \(a,\,\,b\) là các số nguyên tố cùng nhau và \(b > 0\). Khi đó \(a + b\) bằng:
A \(47\)
B \(9\)
C \( - 47\)
D \( - 9\)
- Câu 28 : Biết \({m_0}\) là giá trị của tham số \(m\) để hàm số \(y = \dfrac{{ - mx + 2}}{{x + m}}\) có giá trị nhỏ nhất trên đoạn \(\left[ { - 1;0} \right]\) bằng \( - 3\). Khi đó:
A \({m_0} \in \left( { - 5; - 2} \right)\)
B \({m_0} \in \left( {0;2} \right)\)
C \({m_0} \in \left( { - 2;0} \right)\)
D \({m_0} \in \left( {2;5} \right)\)
- Câu 29 : Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ. Gọi \(M\) và \(m\) tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f\left( {1 - 2\cos x} \right)\) trên \(\left[ {0;\,\,\dfrac{{3\pi }}{2}} \right]\). Giá trị của \(M + m\) bằng
A \(\dfrac{1}{2}\)
B \(\dfrac{3}{2}\)
C \(1\)
D \(2\)
- Câu 30 : Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình dưới. Tìm \(m\) để bất phương trình \(f\left( x \right) \ge \dfrac{{x + 1}}{{x + 2}} + m\) nghiệm đúng với mọi \(x \in \left[ {0;\,\,1} \right].\)
A \(m \ge f\left( 0 \right) - \dfrac{1}{2}\)
B \(m > f\left( 0 \right) - \dfrac{1}{2}\)
C \(m < f\left( 1 \right) - \dfrac{2}{3}\)
D \(m \le f\left( 1 \right) - \dfrac{2}{3}\)
- Câu 31 : Có tất cả bao nhiêu giá trị của tham số \(m\) để giá trị lớn nhất của hàm số \(y = \left| {{x^2} - 2x + m} \right|\) trên đoạn \(\left[ { - 1;2} \right]\) bằng 5.
A \(3\)
B \(1\)
C \(2\)
D \(4\)
- Câu 32 : Một hộp không nắp được làm từ một mảnh các tông theo hình mẫu. Hộp có đáy là một hình vuông cạnh \(x\left( {cm} \right)\), chiều cao \(h\left( {cm} \right)\) và có thể tích là \(500\left( {c{m^3}} \right)\). Hãy tìm độ dài cạnh của hình vuông sao cho chiếc hộp được làm ra tốn ít nhiên liệu nhất.
A \(5\,\,cm\)
B \(10\,\,cm\)
C \(2\,\,cm\)
D \(3\,\,cm\)
- Câu 33 : Cho một tấm nhôm hình vuông cạnh \(2016\left( {cm} \right)\). Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng \(x\left( {cm} \right)\), rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm \(x\) để hộp nhận được có thể tích lớn nhất.
A \(x = 336\).
B \(x = 504\).
C \(x = 672\).
D \(x = 1008\).
- Câu 34 : Tam giác vuông có diện tích lớn nhất là bao nhiêu nếu tổng của một cạnh góc vuông và cạnh huyền bằng hằng số a (a > 0)?
A \(\dfrac{2{{a}^{2}}}{9}\).
B \(\dfrac{{{a^2}}}{{3\sqrt 3 }}\).
C \(\dfrac{{{a^2}}}{{6\sqrt 3 }}\).
D \(\dfrac{{{a^2}}}{9}\)
- Câu 35 : Người ta muốn mạ vàng cho một cái hộp có đáy hình vuông không nắp có thể tích là 4 lít. Tìm kích thước của hộp đó để lượng vàng dùng mạ là ít nhất. Giả sử độ dày của lớp mạ tại mọi nơi trên mặt ngoài hộp là như nhau.
A Cạnh đáy bằng 1, chiều cao bằng 2.
B Cạnh đáy bằng 4, chiều cao bằng 3.
C Cạnh đáy bằng 2, chiều cao bằng 1.
D Cạnh đáy bằng 3, chiều cao bằng 4.
- Câu 36 : Cho một tấm nhôm hình tam giác đều có cạnh bằng \(20\left( {cm} \right)\). Người ta cắt ở ba góc của tấm nhôm đó ba tam giác như hình vẽ dưới đây để được hình chữ nhật MNPQ. Tìm độ dài đoạn MB để hình chữ nhật MNPQ có diện tích lớn nhất.
A \(5\left( {cm} \right)\).
B \(4\left( {cm} \right)\).
C \(2\left( {cm} \right)\).
D \(10\left( {cm} \right)\).
- Câu 37 : Cho một tờ giấy hình chữ nhật với chiều dài \(12{\rm{ }}cm\) và chiểu rộng\(8{\rm{ }}cm\). Gấp góc bên phải của tờ giấy sao cho sau khi gấp, đỉnh của góc đó chạm đáy dưới như hình vẽ. Để độ dài nếp gấp là nhỏ nhất thì giá trị nhỏ nhất đó bằng bao nhiêu?
A \(6\sqrt 3 \).
B \(6\sqrt 2 \).
C \(6\sqrt 5 \).
D \(6\).
- Câu 38 : Một công ty bất động sản có 50 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá \(2\,000\,000\,\) đồng một tháng thì mọi căn hộ đều có người thuê và cứ mỗi lần tăng giá cho thuê mỗi căn hộ thêm \(50\,000\) đồng một tháng thì có thêm một căn hộ bị bỏ trống. Công ty đã tìm ra phương án cho thuê đạt lợi nhuận lớn nhất. Hỏi thu nhập cao nhất công ty có thể đạt được trong 1 tháng là bao nhiêu?
A \(115{\rm{ }}250{\rm{ }}000\).
B \(101{\rm{ }}250{\rm{ }}000\).
C \(100{\rm{ }}000{\rm{ }}000\).
D \(100{\rm{ }}250{\rm{ }}000\).
- Câu 39 : Một cơ sở sản xuất khăn mặt đang bán mỗi chiếc khăn với giá \(30.000\) đồng một chiếc và mỗi tháng cơ sở bán được trung bình \(3000\) chiếc khăn. Cơ sở sản xuất đang có kế hoạch tăng giá bán để có lợi nhận tốt hơn. Sau khi tham khảo thị trường, người quản lý thấy rằng nếu từ mức giá \(30.000\) đồng mà cứ tăng giá thêm \(1000\) đồng thì mỗi tháng sẽ bán ít hơn \(100\) chiếc. Biết vốn sản xuất một chiếc khăn không thay đổi là \(18.000\). Hỏi cơ sở sản xuất phải bán với giá mới là bao nhiêu để đạt lợi nhuận lớn nhất.
A \(39.000\) đồng.
B \(42.000\) đồng
C \(43.000\) đồng.
D \(40.000\) đồng.
- Câu 40 : Một chất điểm chuyển động theo quy luật \(S = - \dfrac{1}{3}{t^3} + 4{t^2} + 9t\) với \(t\) (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và \(S\)(mét) là quãng đường vật chuyển động trong thời gian đó. Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của chất điểm là bao nhiêu?
A \(88\,\,\,\left( {m/s} \right)\).
B \(25\,\,\,\left( {m/s} \right)\).
C \(11\,\,\,\left( {m/s} \right)\).
D \(100\,\,\,\left( {m/s} \right)\).
- - Trắc nghiệm Toán 12 Chương 2 Bài 1 Lũy thừa
- - Trắc nghiệm Toán 12 Chương 2 Bài 2 Hàm số lũy thừa
- - Trắc nghiệm Toán 12 Chương 2 Bài 4 Hàm số mũ và hàm số lôgarit
- - Trắc nghiệm Toán 12 Chương 2 Bài 5 Phương trình mũ và phương trình lôgarit
- - Trắc nghiệm Toán 12 Chương 2 Bài 6 Bất phương trình mũ và bất phương trình lôgarit
- - Trắc nghiệm Toán 12 Chương 3 Bài 1 Nguyên hàm
- - Trắc nghiệm Toán 12 Chương 3 Bài 2 Tích phân
- - Trắc nghiệm Toán 12 Chương 3 Bài 3 Ứng dụng của tích phân trong hình học
- - Trắc nghiệm Toán 12 Bài 1 Số phức
- - Trắc nghiệm Toán 12 Bài 2 Cộng, trừ và nhân số phức

