- Ứng dụng vòng tròn lượng giác trong các bài toán...
- Câu 1 : Một vật dao động điều hoà với phương trình x = 10cos(2πt + π/8)(cm). Biết ở thời điểm t có li độ là 4cm. Li độ dao động ở thời điểm sau đó 0,25s là
A 4cm.
B 2cm.
C -2cm.
D - 4cm.
- Câu 2 : Một vật dao động điều hòa với T. Hãy xác định thời gian ngắn nhất để vật đi từ
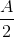đến 
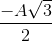
A
B
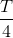
C
D
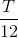
- Câu 3 : Một vật dao động điều hòa với T. Hãy xác định thời gian ngắn nhất để vật đi từ
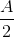theo chiều âm đến vị trí cân bằng theo chiều dương. A
B
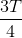
C
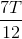
D
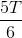
- Câu 4 : Một vật dao động điều hoà với phương trình x = 5cos(10πt) cm. Trong một chu kỳ thời gian vật có tốc độ nhỏ hơn 25π cm/s là:
A
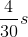
B
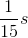
C
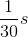
D
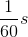
- Câu 5 : Một vật dao động điều hòa với phương trình x = Acos(ωt)cm, chu kì T. Kể từ thời điểm ban đầu thì sau thời gian bằng bao nhiêu lần chu kì, vật qua vị trí cân bằng lần thứ 2012?
A 1006T.
B 1005T +
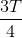
C 1005T +
D 1005T +
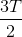
- Câu 6 : Một vật dao động điều hòa trên quỹ đạo dài 20cm. Sau
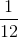(s) kể từ thời điểm ban đầu vật đi được 10cm mà chưa đổi chiều chuyển động và vật đến vị trí có li độ 5cm theo chiều dương. Phương trình dao động của vật là A x = 10 cos(4πt - 2π/3) cm
B x = 10 cos(8πt + 2π/3 ) cm
C x = 10 cos(6πt - π/3) cm
D x = 10 cos(4πt - π/3 ) cm
- Câu 7 : Vật dao động điều hòa theo phương trình x = Acos(
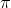t - 
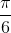) cm. Thời điểm vật đi qua vị trí cân bằng là: A t =
+ 2k (s) k ∈ N B t =
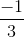+ 2k(s) k ∈ N C t =
+ k (s) k ∈ N D t =
+ k (s) k ∈ N - Câu 8 : Vật dao động với phương trình x = 5cos(4πt +π/6) cm. Tìm thời điểm vật qua vị trí cân bằng lần thứ 4 kể từ thời điểm ban đầu.
A 6/5s
B 4/6s
C 5/6s
D Kết quả khác
- Câu 9 : Một vật dao động điều hoà với phương trình x = 10cos(4πt + π/8)(cm). Biết ở thời điểm t có li độ là -8cm. Li độ dao động ở thời điểm sau đó 13s là
A -8cm.
B 4cm.
C -4cm.
D 8cm.
- Câu 10 : Một vật dao động theo phương trình x = 3cos(5πt - 2π/3) +1(cm). Trong giây đầu tiên vật đi qua vị trí N có x = 1cm mấy lần?
A 2 lần.
B 3 lần.
C 4 lần.
D 5 lần.
- Câu 11 : Một vật dao động điều hòa với chu kì T. Hãy xác định thời gian ngắn nhất để vật đi từ vị trí cân bằng đến vị trí \({{A\sqrt 2 } \over 2}\)
A \({T \over 8}\)
B \({T \over 4}\)
C \({T \over 6}\)
D \({T \over 12}\)
- Câu 12 : Một vật dao động điều hòa với T. Hãy xác định thời gian ngắn nhất để vật đi từ
đến 
A
B
C
D
- Câu 13 : Một vật dao động điều hòa với T. Hãy xác định thời gian ngắn nhất để vật đi từ theo chiều âm đến vị trí cân bằng theo chiều dương.
A
B
C
D
- Câu 14 : Một vật dao động điều hòa với phương trình x = 5cos(4πt - π/2)cm. Xác định thời gian ngắn nhất để vật đi từ vị trí 2,5cm đến -2,5cm.
A
B
C
D
- Câu 15 : Thời gian ngắn nhất để một vật dao động điều hòa với phương trình x = 10cos(πt - π/2) cm đi từ vị trí cân bằng đến vị trí biên
A 2s
B 1s
C 0,5s
D 0,25s.
- Câu 16 : Một vật dao động điều hòa từ A đến B với chu kỳ T, vị trí cân bằng O. Trung điểm OA, OB là M, N. Thời gian ngắn nhất để vật đi từ M đến N là
s. Hãy xác định chu kỳ dao động của vật. A
B
C
D
- Câu 17 : Một vật dao động điều hoà với phương trình x = 4cos(10πt + π/2) cm. Xác định thời điểm đầu tiên vật đi đến vị trí có gia tốc là 20m/s2 và vật đang tiến về vị trí cân bằng
A
B
C
D
- Câu 18 : Một vật dao động điều hoà với phương trình x = 5cos(10πt) cm. Trong một chu kỳ thời gian vật có độ lớn vận tốc nhỏ hơn 25π cm/s là:
A
B
C
D
- Câu 19 : Một vật dao động điều hoà với tần số góc là 10 rad/s và biên độ 2cm. Thời gian mà vật có độ lớn vận tốc nhỏ hơn
cm/s trong mỗi chu kỳ là A
B
C
D
- Câu 20 : Một vật dao động điều hoà với phương trình x =Acos(ωt +π/3 ). Biết quãng đường vật đi được trong thời gian 1(s) là 2A và \(\frac{2}{3}s\) đầu tiên là 9cm. Giá trị của A và ω là
A 9cm và π rad/s.
B 12 cm và 2π rad/s
C 6cm và π rad/s.
D 12cm và π rad/s.
- Câu 21 : Một vật dao động điều hòa với phương trình x = Acos(ωt + π/3), chu kì T. Kể từ thời điểm ban đầu thì sau thời gian bằng bao nhiêu lần chu kì, vật qua vị trí cân bằng theo chiều âm lần thứ 2011?
A 2011T.
B 2010T +
C 2010T.
D 2010T +
- Câu 22 : Một vật dao động điều hòa với phương trình x = Acos(ωt +π/3), chu kì T. Kể từ thời điểm ban đầu thì sau thời gian bằng bao nhiêu lần chu kì, vật qua vị trí cân bằng theo chiều âm lần thứ 2012?
A 2010T.
B 2011T +
C 2011T.
D 2011T +
- Câu 23 : Một vật dao động điều hòa với phương trình x = Acos(ωt + π/6), chu kì T. Kể từ thời điểm ban đầu thì sau thời gian bằng bao nhiêu lần chu kì, vật qua vị trí cách vị trí cân bằng A/2 lần thứ 2001?
A 500T +
B 200T +
C 1000T+
D 200T.
- Câu 24 : Một vật dao động điều hòa trên quỹ đạo dài 20cm. Sau
(s) kể từ thời điểm ban đầu vật đi được 10cm mà chưa đổi chiều chuyển động và vật đến vị trí có li độ 5cm theo chiều dương. Phương trình dao động của vật là A x = 10 cos(4πt - 2π/3) cm
B x = 10 cos(8πt + 2π/3 ) cm
C x = 10 cos(6πt - π/3) cm
D x = 10 cos(4πt - π/3 ) cm
- Câu 25 : Một vật dao động điều hoà với tốc độ cực đại là 10π cm/s. Ban đầu vật đứng ở vị trí có vận tốc là 5π cm/s và thời gian ngắn nhất để vật đi từ vị trí trên đến vị trí có vận tốc v = 0 là 0,1s. Hãy viết phương trình dao động của vật?
A x = 1,2cos(25πt/3 - 5π/6) cm
B x = 1,2cos(25πt/3 +5π/6)cm
C x = 6cos(5πt/3 - π/6)cm
D x = 2,4cos(10πt/3 +π/2)cm
- Câu 26 : Vật dao động điều hòa theo phương trình x = Acos(
t - 
) cm. Thời điểm vật đi qua vị trí cân bằng là: A t =
+ 2k (s) k ∈ N B t =
+ 2k(s) k ∈ N C t =
+ k (s) k ∈ N D t =
+ k (s) k ∈ N - Câu 27 : Vật dao động điều hòa theo phương trình x = Acos(2πt - π/3)cm. Thời điểm vật đi qua vị trí cân bằng theo chiều âm là:
A t =
+ k (s) (k = 1, 2, 3…)B t =
+ k(s) (k = 0, 1, 2…)C t =
+ 
(s) (k = 1, 2, 3…) D t =
+ k(s) (k = 0, 1, 2…) - Câu 28 : Vật dao động điều hòa trên phương trình x = 4cos(4πt + π/6 ) cm. Thời điểm vật đi qua vị trí có li độ x = 2cm theo chiều âm là:
A t =
+ (s) (k = 1, 2, 3..) B t =
+ (s) (k = 0, 1, 2…)C t =
(s) (k = 0, 1, 2…) D t =
+ (s) (k = 1, 2, 3…) - Câu 29 : Vật dao động với phương trình x = 5cos(4πt +π/6) cm. Tìm thời điểm vật đi qua vị trí biên dương lần thứ 4 kể từ thời điểm ban đầu.
A 1,69s
B 1.82s
C 2s
D 1,96s
- Câu 30 : Một vật dao động điều hòa trên trục x’ox với phương trình x = 10cos(πt) cm. Thời điểm để vật qua x = + 5cm theo chiều âm lần thứ hai kể từ t = 0 là:
A
B
C
D 1 (s).
- Câu 31 : Một vật dao động điều hòa với phương trình x = 6cos(4πt + π/3) cm. Tính quãng đường vật đi được sau 1s kể từ thời điểm ban đầu.
A 24 cm
B 60 cm
C 48 cm
D 64 cm
- Câu 32 : Một vật dao động điều hòa với T. Hãy xác định thời gian ngắn nhất để vật đi từ vị trí cân bằng đến \(\frac{{A\sqrt 2 }}{2}\)
A \(\frac{T}{8}\)
B \(\frac{T}{4}\)
C \(\frac{T}{6}\)
D \(\frac{T}{{12}}\)
- Câu 33 : Một vật dao động điều hòa với T. Hãy xác định thời gian ngắn nhất để vật đi từ \(\frac{A}{2}\) đến \(\frac{{ - A\sqrt 3 }}{2}\)
A \(\frac{T}{8}\)
B \(\frac{T}{4}\)
C \(\frac{T}{6}\)
D \(\frac{T}{{12}}\)
- Câu 34 : Một vật dao động điều hòa với chu kì T. Hãy xác định thời gian ngắn nhất để vật đi từ \(\frac{A}{2}\) theo chiều âm đến vị trí cân bằng theo chiều dương.
A \(\frac{T}{2}\)
B \(\frac{{3T}}{4}\)
C \(\frac{{7T}}{{12}}\)
D \(\frac{{5T}}{6}\)
- Câu 35 : Một vật dao động điều hòa với phương trình \(x = 5\cos \left( {4\pi t - \frac{\pi }{2}} \right)\,\,cm\). Xác định thời gian ngắn nhất để vật đi từ vị trí 2,5cm đến – 2,5 cm.
A \(\frac{1}{{12}}s\)
B \(\frac{1}{{10}}s\)
C \(\frac{1}{{20}}s\)
D \(\frac{1}{6}s\)
- Câu 36 : Thời gian ngắn nhất để một vật dao động điều hòa với phương trình \(x = 10\cos \left( {\pi t - \frac{\pi }{2}} \right)\,\,cm\) đi từ vị trí cân bằng đến vị trí biên là
A 2 s
B 1 s
C 0,5 s
D 0,25 s
- Câu 37 : Một vật dao động điều hòa từ A đến B với chu kỳ T, vị trí cân bằng O. Trung điểm OA, OB là M, N. Thời gian ngắn nhất để vật đi từ M đến N là \(\frac{1}{{30}}s\). Hãy xác định chu kỳ dao động của vật.
A \(\frac{1}{4}s\)
B \(\frac{1}{5}s\)
C \(\frac{1}{{10}}s\)
D \(\frac{1}{6}s\)
- Câu 38 : Một vật dao động điều hoà với phương trình \(x = 4\cos \left( {10\pi t + \frac{\pi }{2}} \right)\,\,cm\). Xác định thời điểm đầu tiên vật đi đến vị trí có gia tốc là \(20m/{s^2}\) và vật đang tiến về vị trí cân bằng
A \(\frac{1}{{12}}s\)
B \(\frac{1}{{60}}s\)
C \(\frac{1}{{10}}s\)
D \(\frac{1}{{30}}s\)
- Câu 39 : Một vật dao động điều hòa với phương trình \(x = A\cos \left( {\omega t + \frac{\pi }{3}} \right)\), chu kì T. Kể từ thời điểm ban đầu, sau thời gian bằng bao nhiêu lần chu kì, vật qua vị trí cân bằng theo chiều âm lần thứ 2011?
A \(2011T\).
B \(2010T + \frac{T}{{12}}\).
C \(2010T\)
D \(2010T + \frac{{7T}}{{12}}\)
- Câu 40 : Một vật dao động điều hòa với phương trình \(x = A\cos \left( {\omega t + \frac{\pi }{3}} \right)\), chu kì T. Kể từ thời điểm ban đầu, sau thời gian bằng bao nhiêu lần chu kì, vật qua vị trí cân bằng theo chiều âm lần thứ 2012?
A \(2011T\).
B \(2011T + \frac{T}{{12}}\).
C \(2011T\).
D \(2011T + \frac{{7T}}{{12}}\).
- Câu 41 : Một vật dao động điều hòa với phương trình \(x = A\cos \left( {\omega t} \right)\,\,cm\), chu kì T. Kể từ thời điểm ban đầu, sau thời gian bằng bao nhiêu lần chu kì, vật qua vị trí cân bằng lần thứ 2012?
A \(1006T\).
B \(1005T + \frac{{3T}}{4}\).
C \(1005T + \frac{T}{2}\).
D \(1005T + \frac{{3T}}{2}\).
- Câu 42 : Một vật dao động điều hòa với phương trình \(x = A\cos \left( {\omega t + \frac{\pi }{6}} \right)\), chu kì T. Kể từ thời điểm ban đầu thì sau thời gian bằng bao nhiêu lần chu kì, vật qua vị trí cách vị trí cân bằng \(\frac{A}{2}\) lần thứ 2001?
A \(500T + \frac{T}{{12}}\).
B \(200T + \frac{T}{{12}}\).
C \(500T\).
D \(200T\).
- Câu 43 : Một vật dao động điều hòa trên quỹ đạo dài 20 cm. Sau \(\frac{1}{{12}}s\) kể từ thời điểm ban đầu, vật đi được 10 cm mà chưa đổi chiều chuyển động và vật đến vị trí có li độ 5 cm theo chiều dương. Phương trình dao động của vật là
A \(x = 10\cos \left( {4\pi t - \frac{{2\pi }}{3}} \right)\,\,cm\).
B \(x = 10\cos \left( {6\pi t - \frac{{2\pi }}{3}} \right)\,\,cm\).
C \(x = 10\cos \left( {6\pi t - \frac{\pi }{3}} \right)\,\,cm\).
D \(x = 10\cos \left( {4\pi t - \frac{\pi }{3}} \right)\,\,cm\).
- Câu 44 : Vật dao động điều hòa theo phương trình \(x = A\cos \left( {\pi t - \frac{\pi }{6}} \right)\,\,cm\). Thời điểm vật đi qua vị trí cân bằng là:
A \(t = \frac{2}{3} + 2k\,\left( s \right)\,\,\left( {k \in N} \right)\).
B \(t = - \frac{1}{3} + 2k\,\,\left( s \right)\,\,\left( {k \in N} \right)\).
C \(t = \frac{2}{3} + k\,\,\left( s \right)\,\,\left( {k \in N} \right)\).
D \(t = \frac{1}{3} + k\,\,\left( s \right)\,\,\left( {k \in N} \right)\).
- Câu 45 : Vật dao động điều hòa theo phương trình \(x = A\cos \left( {2\pi t - \frac{\pi }{3}} \right)\,\,cm\). Thời điểm vật đi qua vị trí cân bằng theo chiều âm là:
A \(t = - \frac{1}{{12}} + k\,\,\left( s \right)\,\,\left( {k = 0,1,2...} \right)\).
B \(t = \frac{5}{{12}} + k\,\,\left( s \right)\,\,\left( {k = 0,1,2...} \right)\).
C \(t = - \frac{1}{{12}} + \frac{k}{2}\,\,\left( s \right)\,\,\left( {k = 0,1,2...} \right)\)
D \(t = \frac{1}{{15}} + k\,\,\left( s \right)\,\,\left( {k = 0,1,2...} \right)\).
- Câu 46 : Vật dao động điều hòa trên phương trình \(x = 4\cos \left( {4\pi t + \frac{\pi }{6}} \right)\,\,cm\). Thời điểm vật đi qua vị trí có li độ x = 2 cm theo chiều âm là:
A \(t = - \frac{1}{8} + \frac{k}{2}\,\,\left( s \right)\,\,\left( {k = 1,2,3...} \right)\).
B \(t = \frac{1}{{24}} + \frac{k}{2}\,\,\left( s \right)\,\,\left( {k = 0,1,2...} \right)\).
C \(t = \frac{k}{2}\,\,\left( s \right)\,\,\left( {k = 0,1,2...} \right)\).
D \(t = - \frac{1}{6} + \frac{k}{2}\,\,\left( s \right)\,\,\left( {k = 1,2,3...} \right)\).
- Câu 47 : Vật dao động với phương trình \(x = 5\cos \left( {4\pi t + \frac{\pi }{6}} \right)\,\,cm\). Tìm thời điểm vật đi qua vị trí biên dương lần thứ 4 kể từ thời điểm ban đầu.
A 1,69 s.
B 1,82 s.
C 2 s.
D 1,96 s.
- Câu 48 : Vật dao động với phương trình \(x = 5\cos \left( {4\pi t + \frac{\pi }{6}} \right)\,\,cm\). Tìm thời điểm vật qua vị trí cân bằng lần thứ 4 kể từ thời điểm ban đầu.
A \(\frac{6}{5}\,\,s\).
B \(\frac{4}{6}\,\,s\).
C \(\frac{5}{6}\,\,s\).
D Kết quả khác.
- Câu 49 : Vật dao động điều hòa có vận tốc cực đại bằng 3 m/s và gia tốc cực đại bằng \(30\pi \,\,m/{s^2}\). Thời điểm ban đầu vật có vận tốc 1,5 m/s và thế năng đang giảm. Hỏi vào thời điểm nào sau đây vật có gia tốc bằng \( - 15\pi \,\,m/{s^2}\)
A 0,10 s.
B 0,05 s.
C 0,15 s.
D 0,20 s.
- Câu 50 : Một con lắc lò xo đang dao động điều hòa với biên độ A, thời gian ngắn nhất để con lắc di chuyển từ vị trí có li độ \({x_1} = - A\) đến vị trí có li độ \({x_2} = \frac{A}{2}\) là 1s. Chu kì dao động của con lắc là
A \(\frac{1}{3}\,\,s\).
B 2 s.
C 3 s.
D 6 s.
- Câu 51 : Một vật dao động điều hòa với phương trình \(x = 10\cos 10\pi t\,\,cm\). Khoảng thời gian vật đi từ vị trí có li độ x = 5 cm từ lần thứ 2014 đến lần thứ 2015 là:
A \(\frac{1}{5}\,\,s\).
B \(\frac{2}{{15}}\,\,s\).
C \(\frac{1}{{15}}\,\,s\) .
D \(\frac{4}{{15}}\,\,s\).
- - Trắc nghiệm Vật lý 12 Bài 2 Con lắc lò xo
- - Trắc nghiệm Vật lý 12 Bài 4 Dao động tắt dần và dao động cưỡng bức
- - Trắc nghiệm Vật lý 12 Bài 5 Tổng hợp hai dao động điều hòa cùng phương, cùng tần số và Phương pháp Fre-Nen
- - Trắc nghiệm Vật lý 12 Bài 7 Sóng cơ và sự truyền sóng cơ
- - Trắc nghiệm Vật lý 12 Bài 9 Sóng dừng
- - Trắc nghiệm Vật lý 12 Bài 12 Đại cương về dòng điện xoay chiều
- - Trắc nghiệm Vật lý 12 Bài 13 Các mạch điện xoay chiều
- - Trắc nghiệm Vật lý 12 Bài 14 Mạch có R, L, C mắc nối tiếp
- - Trắc nghiệm Vật lý 12 Bài 16 Truyền tải điện năng và máy biến áp
- - Trắc nghiệm Vật lý 12 Bài 15 Công suất điện tiêu thụ của mạch điện xoay chiều và Hệ số công suất
Liên kết với Facebook
Liên kết với Google