Những kiến thức cần biết trong giải Toán về bất phương trình Logarit
Những kiến thức cần biết trong giải toán về bất phương trình Logarit
Dạng toán về bất phương trình logarit một dạng bài hết sức cơ bản và thường xuất hiện trong đề thi. Tuy nhiên, nhiều bạn thấy bất phương trình logarit khó và nó lại gây không ít khó khăn cho học sinh trong quá trình tìm hiểu phương pháp giải. Nhận thấy được điều đó, chúng tôi đã soạn lên bài giảng này với hy vọng giúp đỡ được các bạn trong học tập, đặc biệt là môn Toán!
I. Tổng quát
- Khái niệm
Bất phương trình logarit cơ bản có dạng:
\(log_a^x > b (hoặc \ log_a^x < b; log_a^x ≥b; log_a^x ≤ b)\) với điều kiện a,b là hai số đã cho,a>0, a≠1
Để giải các bất phương trình dạng cơ bản ta chỉ cần biến đổi phương trình gốc thành một số dạng như sau:
- Nếu a > 1 thì:
\(log_a^x > b ⇔ alog_a^xalog_a^x > a^b ⇔ x > a^b ; \)
\(log_a^x ≥ b ⇔ x ≥ a^b\)
\(log_a^x < b ⇔ 0 < x < a^b ;\)
\(log_a^x ≤ b ⇔ 0 < x ≤ a^b\)
- Nếu 0 < a< 1 thì
\(log_a^x ≤ b ⇔ 0 < x ≤ a^b\)
\(log_a^x ≤ b ⇔ 0 < x ≤ a^b\)
\(log_a^x ≥ b ⇔ 0 < x ≤ a^b\)
\(log_a^x < b ⇔ x > a^b ;\)
\(log_a^x ≤ b ⇔ x ≥ a^b\)
Để tìm m để bất phương trình logarit có nghiệm, trước tiên ta cần tìm x để bất phương trình xác định. Hàm số cho trước có thể là hàm số chứa căn, hàm phân số,...
II. Cách giải bất phương trình logarit chứa tham số
1. Giải bất phương trình logarit khác cơ số
Bất phương trình logarit với cơ số khác nhau luôn là vấn đề gây khó dễ cho học sinh khi gặp phải trong các đề thi. Học sinh thường lúng túng khi biến đổi, gặp khó khăn để đưa về cùng cơ số hoặc đưa về các phương trình cơ bản.
Tương tự như phương trình ta có:
\(log_a^x ≥ log_a^{g(x)} ⇔ f(x) ≥ g(x)\)
Ví dụ: Giải bất phương trình sau: \(log_5(3 + \sqrt x)> log_4x\)
Ta có:
\(log_4x = t \Rightarrow x = 4^t \Rightarrow log_5(3+2^t) > t \Rightarrow 3+2^t > 5^t\Rightarrow 3(\frac{1}{5})^t + (\frac{2}{5})^t > 1\) nhận thấy vế trái là hàm nghịch biến
\(f(1) = 1 \Rightarrow t < 1 \Rightarrow log_4x < 1 \\ \\ 0 < x < 4\)
2. Cách giải bất phương trình logarit bằng máy tính
Để tìm tập nghiệm của bất phương trình logarit ta sử dụng máy tính Casio để giải. Mời các bạn tham khảo phương pháp bấm máy dưới video sau:
Ví dụ: Giải bất phương trình: \(log_{\dfrac{1}{2}}\dfrac{x^2−3x+2}{x}≥0 \)bằng máy tính?
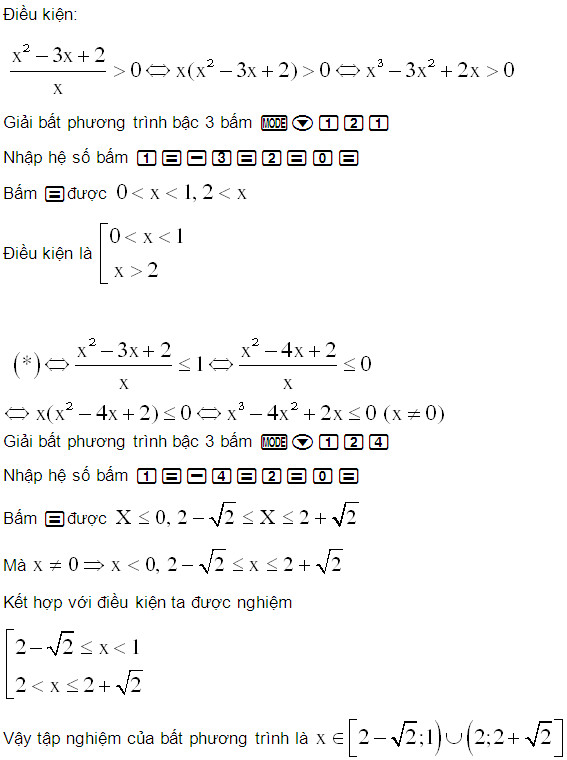
III. Bài tập bất phương trình logarit có lời giải
Trên đây là toàn bộ kiến thức chúng tôi muốn chia sẻ về bất phương trình logarit, cùng học vui chúc các bạn đạt được điểm số cao!

