Mẹo Toán học - Tìm tập xác định của hàm số logarit

Mẹo Toán học - Tìm tập xác định của hàm số logarit

Dạng toán về tìm tập xác định của hàm số logarit là một dạng bài hết sức cơ bản và thường xuất hiện trong đề thi trong đó hàm số logarit cũng là một dạng rất quan trọng không thể bỏ qua. Tuy nhiên, nó lại gây không ít khó khăn cho học sinh trong quá trình tìm hiểu phương pháp giải. Nhận thấy được điều đó, chúng tôi đã soạn lên bài giảng này với hy vọng giúp đỡ được các bạn trong học tập, đặc biệt là môn Toán!

I. Định nghĩa về tập xác định

Tập xác định của một hàm số cho trước được định nghĩa là tất cả các giá trị thích hợp làm cho biểu thức đã cho có nghĩa và luôn tìm được một giá trị xác định. Biểu thức đó có thể được cho dưới dạng căn bậc hai, lũy thừa, phân số...Bằng cách áp dụng các phương pháp cơ bản chúng ta có thể tìm ra được các giá trị thích hợp của biến số.

Ví dụ: Hàm số y = \(\sqrt{x-1}\) xác định khi x - 1 lớn hơn hoặc bằng 0 suy ra x lớn hơn hoặc bằng 1.

II. Các dạng phổ biến thường gặp

    1. Tìm tập xác định của hàm chứa phân số

Trường hợp hàm logarit đã cho ở dưới dạng phân số thì hàm được xác định khi mẫu số khác 0.

Tổng quát: \(y =log_a^{\dfrac{f(x)}{g(x)}}\) xác định \(\Leftrightarrow g(x)\neq 0\)

Ví dụ: Tìm tập xác định của hàm logarit sau đây: \(y=log_2{\dfrac{x}{x-1}}\)

Hàm số xác định khi x-1 # 0 suy ra x # 1.

    2. Cách tìm tập xác định của hàm số logarit chứa căn

Trường hợp hàm logarit đã cho có chứa căn thì hàm xác định khi biểu thức trong căn lớn hơn hoặc bằng 0.

Tổng quát: \(y = \sqrt{f(x)-g(x)}\) xác định \(\Leftrightarrow f(x)-g(x) \ge 0\Leftrightarrow f(x)\ge g(x)\)

Xem ngay:

• Số trung bình cộng. Số trung vị. Mốt
• Phương sai và độ lệch chuẩn

III. Bài tập tìm tập xác định của hàm số logarit

Bài 1:

Bài 2: Tìm tập xác định của hàm số mũ và logarit sau:

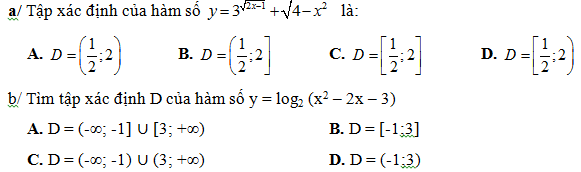
Trên đây là toàn bộ kiến thức chúng tôi muốn chia sẻ về phương pháp tìm tập xác định của hàm số logarit, cùng học vui chúc các bạn đạt được điểm số cao!