Lý thuyết về tâm đường trọn nội tiếp tam giác chuẩn nhất

Cunghocvui gửi đến bạn bài viết tổng hợp các kiến thức lý thuyết về tâm đường tròn nội tiếp tam giác như cách tâm đường tròn nội tiếp tam giác vuông, tâm đường tròn nội tiếp tam giác đều, công thức tính bán kính đường tròn nội tiếp tam giác. 

I) Đường tròn nội tiếp tam giác

1) Khái niệm

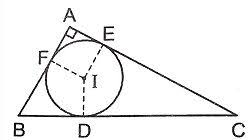
Đường tròn nội tiếp tam giác là khi ba cạnh của tam giác là tiếp tuyến của đường tròn và đường tròn nằm hoàn toàn bên trong tam giác.

2) Cách xác định tâm đường tròn nội tiếp tam giác

Để xác định được không chỉ tâm đường tròn nội tiếp tam giác vuông mà còn tâm đường tròn nội tiếp tam giác đều nữa thì ta cần ghi nhớ lý thuyết.

Với tâm đường tròn nội tiếp của tam giác là giao điểm ba đường phân giác trong của tam giác, hoặc có thể là hai đường phân giác.

II) Bán kính đường tròn nội tiếp tam giác

Tam giác ABC có độ dài lần lượt là a, b, c ứng với ba cạnh BC. AC, AB.

- Nửa chu vi tam giác

\(p = \dfrac {a+b+c} {2}\)

- Bán kính đường tròn nội tiếp tam giác

\(r = \dfrac {2S}{a+b+c} =\sqrt{\dfrac {(p-a)(p-b)(p-c)}{p}}\)

III) Bài tập

Bài 1: Trong tam giác ABC có AB = 3cm, AC = 7cm, BC = 8cm. Bán kính r đường tròn nội tiếp tam giác ABC bằng?

Hướng dẫn

- Chu vi tam giác ABC: p = 9.

- Bán kính:  \(r = \dfrac {2\sqrt{3}} {3}\)

Bài 2: Cho ba điểm có tọa độ như sau: \(A(-2; 3); B(\dfrac {1}{4}; 0); C(2; 0)\) nằm trong mặt phẳng Oxy. Hãy tìm tâm đường tròn nội tiếp tam giác ABC.

Trên đây là bài viết mà Cunghocvui đã tổng hợp được về tâm đường tròn nội tiếp tam giác, hãy để lại comment đáp án bài tập và những ý kiến thắc mắc của bạn ở phía dưới nhé!