Phương pháp tìm tập xác định của hàm số lũy thừa cần biết

Phương pháp tìm tập xác định của hàm số lũy thừa cần biết

Dạng toán về tập xác định của một hàm số lũy thừa là một dạng bài hết sức cơ bản và thường xuất hiện trong đề thi. Tuy nhiên, nó lại gây không ít khó khăn cho học sinh trong quá trình tìm hiểu phương pháp giải. Nhận thấy được điều đó, chúng tôi đã soạn lên bài giảng này với hy vọng giúp đỡ được các bạn trong học tập, đặc biệt là môn Toán!

I. Định nghĩa

Tập xác định của một hàm số cho trước hay còn gọi là miền xác định là tập hợp các giá trị thích hợp thỏa mãn biến số, làm cho hàm số đã cho có giá trị xác định. Tập xác định gồm rất nhiều giá trị, nên chúng ta cần phải tìm ra giá trị chính xác giúp hàm số đó cho nghĩa.

II. Các dạng phổ biến thường gặp

    1. Tìm tập xác định của hàm số mũ nguyên âm

Công thức tổng quát:

Xét hàm số \(y = [f(x)]α\)

    • Khi α > 0: hàm số xác định khi và chỉ khi f(x) xác định.

    • Khi α < 0: hàm số xác định khi và chỉ khi f(x) ≠ 0.

    • Khi α không nguyên: hàm số xác định khi và chỉ khi f(x) > 0.

Tương tự với dạng bài tìm tập xác định của hàm số mũ không nguyên.

Ví dụ:

Tìm tập xác định D của hàm số \(y=(x^2-1)^{-8}\)

Lời giải:

Hàm số trên xác định tại: \(x^2-1 ≠ 0 ⇔ x ≠ ±1\)

Bài tập liên quan:

• Tập hợp
• Các phép toán tập hợp

    2. Cách tìm tập xác định của hàm số lũy thừa

Hàm số lũy thừa tổng quát có dạng \(y = {x^\alpha }\left( {\alpha  \in R} \right)\). Các hàm số lũy thừa có tập xác định khác nhau, tùy theo \(\alpha\) trong các trường hợp sau: 

- Nếu \(\alpha\) > 0 thì tập các định là R.

- Nếu \(\alpha\) < 0 hoặc \(\alpha\) = 0 thì tập các định là \(R\backslash \left\{ 0 \right\}\).

- Nếu\(\alpha\) không nguyên thì tập các định là \(\left( {0; + \infty } \right)\).

Lưu ý: Hàm số \(y = \sqrt x \) có tập xác định là \(\left[ {0; + \infty } \right), hàm \ số \ y = \sqrt[3]{x}\) có tập xác định R, trong khi đó các hàm \( y = {x^{\frac{1}{2}}},y = {x^{\frac{1}{3}}}\) đều có tập xác định (0; +∞). Vì vậy\( y = \sqrt x \ và \ y = {x^{\frac{1}{2}}} ( hay \ y = \sqrt[3]{x} \ và \ y = {x^{\frac{1}{3}}})\) là những hàm số khác nhau.

III. Bài tập tìm tập xác định của hàm số lũy thừa

Để nắm chắc dạng bài tập này các bạn có thể tham khảo thêm các bài tập liên quan về tìm tập xác định của hàm số, xem thêm tại trang web cunghocvui.com.

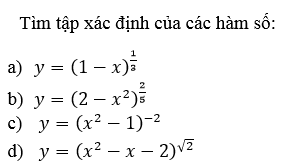
Trên đây là toàn bộ kiến thức chúng tôi muốn chia sẻ, hy vọng rằng với bộ kiến thức trên sẽ giúp các bạn làm chủ được các dạng bài tập liên quan đến tìm tập xác định của hàm số lũy thừa. Cùng học vui chúc các bạn đạt được điểm số cao!