Lý thuyết Tính chất của hai tiếp tuyến cắt nhau chi tiết nhất

Bài giảng tính chất của hai tiếp tuyến cắt nhau là một trong những bài kiến thức quan trọng về tiếp tuyến thuộc chương II Đường tròn. Cunghocvui xin gửi tới các bạn bài tổng hợp lý thuyết và các dạng bài tập tự luận về các tính chất của hai tiếp tuyến cắt nhau đầy đủ và chi tiết. 

A. Một vài kiến thức cần nhớ về các tính chất của hai tiếp tuyến cắt nhau

1. Một số định lý về hai tiếp tuyến cắt nhau trong phạm vi một đường tròn. Nêu tính chất của hai tiếp tuyến cắt nhau?

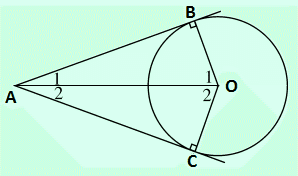
Trong phạm vi là một đường tròn, nếu hai tiếp tuyến của một đường tròn giao cắt nhau tại một điểm thì điểm đó có những tính chất sau đây:

- Khoảng cách độ dài từ điểm giao cắt đến hai tiếp điểm nằm trên đường tròn là bằng nhau (\(AB=AC\)).

- Tia được tạo bởi điểm giao cắt và tâm có tính chất chia góc được tạo bởi hai tiếp tuyến thành hai góc bằng nhau (\(AO\) là tia phân giác của \(\widehat{BAC}\)).

- Tia được tạo bởi tâm và điểm giao cắt cũng có tính chất chia góc được tạo bởi tâm và hai bán kính đi qua hai tiếp điểm là bằng nhau (\(AO\) là tia phân giác của \(\widehat{BOC}\).

2. Các kiến thức về đường tròn nội tiếp tam giác

Một đường tròn được gọi là nội tiếp tam giác có những tính chất sau đây:

- Tâm đường tròn nội tiếp là điểm giao cắt của ba đường phân giác góc trong của ba góc trong tam giác. 

- Đường tròn nội tiếp tiếp xúc với ba cạnh của tam giác, tam giác có đường tròn tiếp xúc đó được gọi là tam giác ngoại tiếp đường tròn.

3. Các kiến thức về đường tròn bàng tiếp tam giác

Một đường tròn được gọi là bàng tiếp tam giác có những tính chất sau đây:

- Tâm của đường tròn bàng tiếp tam giác là điểm giao cắt của một đường phân giác góc trong và hai đường phân giác góc ngoài trong một tam giác.

- Đường tròn bàng tiếp tam giác tiếp xúc với đường kéo dài của hai trong ba cạnh của một tam giác.

- Có ba đường tròn bàng tiếp một tam giác (ứng với ba đỉnh của tam giác). Ví dụ đường tròn bàng tiếp góc \(\widehat{A}\) của tam giác \(ABC\) có tâm đường tròn là giao điểm của đường phân giác góc trong \(\widehat{A}\) và hai góc ngoài \(\widehat{B}\) và \(\widehat{C}\). 

B. Tính chất của hai tiếp tuyến cắt nhau luyện tập

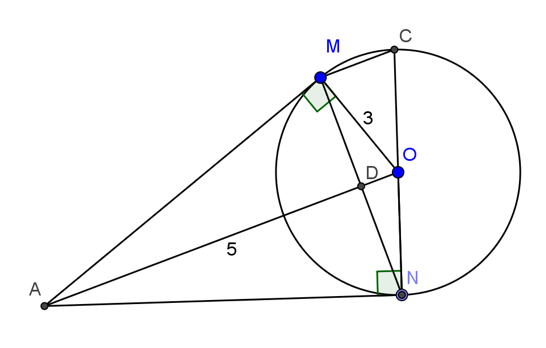
Bài 1: Cho một đường tròn có tâm O và một điểm A không thuộc đường tròn. Xuất phát từ điểm A, kẻ đồng thời hai tiếp tuyến \(AM\) và \(AN\) tới đường tròn (với \(M\) và \(N\) là hai tiếp điểm). Hãy:

a, Hãy sáng tỏ rằng \(OA\perp MN\)

b, Kẻ một đường kính \(NC\). Hãy sáng tỏ rằng \(MC//AO\)

c, Giả sử độ dài của tia \(OM\) bằng 3cm, tia \(OA\) bằng 5cm, hỏi các cạnh của tam giác \(AMN\) có độ dài bao nhiêu?

Hướng dẫn làm bài tập: 

a, Theo tính chất của hai tiếp tuyến cắt nhau trong phạm vi một đường tròn ở mục 1, ta có : \(AM=AN\)

Và \(OM=ON=R\) 

Xét trong hai tam giác là \(OMD\) và tam giác \(OND\) ta có: 

\(\widehat{MOD}\) = \(\widehat{NOD}\) (\(OA\) là phân giác của \(\widehat{MON}\))

\(OD \) chung

\(OM=ON\)

=> \(\Delta MOD=\Delta NOD\) (theo trường hợp cạnh - góc - cạnh) => \(\widehat{ODM}\) = \(\widehat{ODN}\) mà hai góc này có tổng bằng \(180^0\) => \(\widehat{ODM}\) = \(\widehat{ODN}\) = \(90^0\) 

=> \(OA\perp MN\) (Điều phải chứng minh)

b, Xét trong phạm vi của tam giác \(MNC\) ta có: \(\widehat{NMC}=90^0\) (góc chắn nửa đường tròn) 

=> \(MN\perp MC\)

Mà theo ý a, \(OA\perp MN\) => \(OA//MC\) (vì cùng tạo với \(MN\) một góc bằng \(90^0\))

c, Xét trong phạm vi tam giác vuông \(AMO\) có \(\widehat{AMO}=90^0\), áp dụng định lý Py-ta-go trong tam giác vuông ta có:

\(AM^2=OA^2-OM^2\) = \(5^2-3^2=16\) => \(AM=\sqrt{16}=4(cm)\)

Theo tính chất của hai tiếp tuyến cắt nhau trong phạm vi một đường tròn ở mục 1, ta có : \(AM=AN\)

=> \(AN=4(cm)\)

 Với tam giác vuông \(AMO\) có \(\widehat{AMO}=90^0\), ta có:

\(OA.MD=AM.MO\) => \(5.MD=4.3\) => \(MD=\dfrac{12}{5}\)

Vì \(MN\) nhận điểm D là trung điểm nên \(MN=2MD\) => \(MN=2.\dfrac{12}{5}=\dfrac{24}{5}\)(cm)

Vậy trong phạm vi tam giác \(AMN\) có \(AM=AN=4(cm)\), \(MN=\dfrac{24}{5}(cm)\)

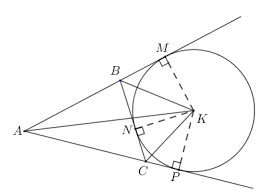
Bài 2: Cho một đường tròn có tâm O và một điểm M không thuộc đường tròn. Xuất phát từ điểm M, kẻ đồng thời hai tiếp tuyến \(MD\) và \(ME\) tới đường tròn (với \(D\) và \(E\) là hai tiếp điểm). Trên dây cung nhỏ \(DE\), lấy một điểm I bất kỳ. Qua I, kẻ một tiếp tuyến với đường tròn, tiếp tuyến này giao với hai tiếp tuyến \(MD\) và \(ME\) tại hai điểm lần lượt là \(P\) và \(Q\). Giả sử độ dài đoạn thẳng \(MD \) bằng 4cm, hỏi chu vi của tam giác \(MPQ\) là bao nhiêu?

Ta có:

+ Đường tròn tâm O nhận \(PD\) và \(PI\) là hai tiếp tuyến với hai tiếp điểm \(D\) và \(I\) 

=> \(PD=PI\) (theo tính chất của hai tiếp tuyến tại mục 1)

+ Đường tròn tâm O nhận \(QI\) và \(QE\) là hai tiếp tuyến với hai tiếp điểm \(E\) và \(I\) 

=> \(QI=QE\) (theo tính chất của hai tiếp tuyến tại mục 1)

+ Đường tròn tâm O nhận \(MD\) và \(ME\) là hai tiếp tuyến với hai tiếp điểm \(D\) và \(E\) 

=> \(MD=ME\) (theo tính chất của hai tiếp tuyến tại mục 1)

Chu vi của tam giác \(MPQ\) = \(MP+PQ+MQ\)

\(MP+PQ+MQ\) = \(MD-PD+ME-QE+PI+IQ\) = \(MD+ME\) = \(2.MD\)

=> \(MP+PQ+MQ\) = \(2.4=8(cm)\)

Vậy chu vi của tam giác \(MPQ\) là 8 (cm)

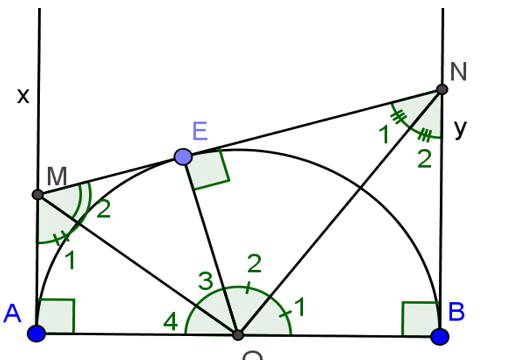
Bài 3: Cho một nửa đường đường tròn với tâm O và một đường kính \(AB\). TỪ hai đầu mút A và B kẻ hai tia \(Ax\) và \(By\) (cùng một bờ mặt phẳng) sao cho hai tia này cùng tạo với đường kính \(AB\) một góc bằng \(90^0\). Trên tia \(Ax\) lấy một điểm M bất kỳ, xuất phát từ điểm M kẻ mọt tiếp tuyến \(ME\) đến nửa đường tròn, tiếp tuyến này cắt tia \(By\) tại N. Hãy:

a, Tính độ lớn của góc \(\widehat{MON}\)

b, Sáng tỏ nhận định \(MN=AM+BN\)

c, Sáng tỏ nhận định \(AM.BN=R^2\) (với \(R\) là bán kính của nửa đường tròn tâm O)

Hướng dẫn giải bài tập:

+ Đường tròn tâm O nhận \(NB\) và \(NE\) là hai tiếp tuyến với hai tiếp điểm \(E\) và \(B\)

=> \(\widehat{ENO}=\widehat{BNO}\) và hai cặp cạnh bằng nhau là \(OE=OB\) và \(NB=NE\) (theo tính chất của hai tiếp tuyến tại mục 1)

+ Đường tròn tâm O nhận \(ME\) và \(MA\) là hai tiếp tuyến với hai tiếp điểm \(E\) và \(A\) 

=> \(\widehat{EMO}=\widehat{AMO}\) và \(\widehat{EOM}=\widehat{MOA}\) và hai cặp cạnh bằng nhau là \(OE=OA\) và \(ME=MA\) (theo tính chất của hai tiếp tuyến tại mục 1)

Ta có: \(\widehat{O_{1}}+\widehat{O_{2}}+\widehat{O_{3}}+\widehat{O_{4}}=180^0\)

Mà ta vừa chứng minh được là \(\widehat{O_{1}}=\widehat{O_{2}}\), \(\widehat{O_{3}}=\widehat{O_{4}}\) => \(2\widehat{O_{2}}+2\widehat{O_{3}}=180^0\) => \(\widehat{O_{2}}+\widehat{O_{3}}=90^0\)

=> \(\widehat{MON}=90^0\) (điều phải chứng minh)

b, Ta có: \(MN=ME+NE=AM+BN\) (chứng minh theo ý a)

c, Trong tam giác vuông \(AMO\) có \(\widehat{AMO}+\widehat{MOA}=90^0\) (hai góc phụ nhau trong một tam giác vuông) mà \(\widehat{AMO}=\widehat{OME}\) (theo tính chất của hai tiếp tuyến tại mục 1)

=> \(\widehat{M_{2}}+\widehat{O_{4}}=90^0\) 

Mặt khác, trong tam giác vuông \(MON\) có \(\widehat{O}=90^0\) (theo ý a) ta có \(\widehat{M_{2}}+\widehat{N_{1}}=90^0\) 

=> \(\widehat{O_{4}}=\widehat{N_{1}}\) (cùng phụ với góc \(\widehat{M_{2}}\)) mà \(\widehat{N_{2}}=\widehat{N_{1}}\) (theo tính chất của hai tiếp tuyến tại mục 1) nên \(\widehat{N_{2}}=\widehat{O_{4}}\) (vì cùng bằng \(\widehat{N_{1}}\))

Xét trong hai tam giác là \(MAO\) và tam giác \(OBN\) ta có: 

\(\widehat{MAO}\) = \(\widehat{OBN}=90^0\) 

\(\widehat{N_{2}}=\widehat{O_{4}}\)

=> \(\Delta MAO=\Delta OBN\) (theo trường học góc - góc)

=> \(MA.BN=OA.OB\) => \(MA.BN=R^2\) (điều phải chứng minh)

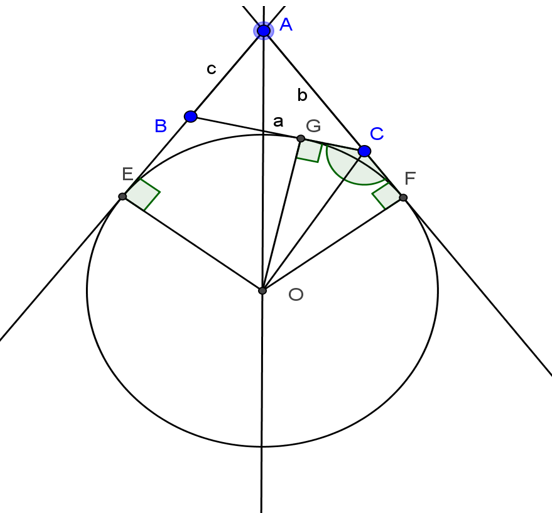
Bài 4: Với \(ABC\) là một tam giác, cho đường tròn bàng tiếp tam giác trong góc A với tâm là K. Đường tròn bàng tiếp này tiếp xúc với hai tia \(AC\) và \(AB\) kéo dài lần lượt tại hai điểm là \(F\) và \(E\). Gọi độ dài đoạn thẳng \(BC\), \(AB\) và \(AC\) lần lượt là a, c và b. Hãy:

a, Sáng tỏ đẳng thức: \(AE=AF=(a+b+c):2\)

b, Sáng tỏ đẳng thức: \(BE=(a+b-c):2\)

c. Sáng tỏ đẳng thức: \(CF=(a-b+c):2\)

Hướng dẫn làm bài tập: 

+ Đường tròn tâm O \(AE\) và \(AF\) là hai tiếp tuyến với hai tiếp điểm O với \(E\) và \(F\) là hai tiếp điểm 

=> \(AE=AF\) (theo tính chất của hai tiếp tuyến tại mục 1)

+ Đường tròn tâm O \(CG\) và \(CF\) là hai tiếp tuyến với hai tiếp điểm \(G\) và \(F\) là hai tiếp điểm 

=> \(CG=CF\) (theo tính chất của hai tiếp tuyến tại mục 1)

+ Đường tròn tâm O \(BE\) và \(BG\) là hai tiếp tuyến với hai tiếp điểm \(D\) và \(I\)  

=> \(BE=BG\) (theo tính chất của hai tiếp tuyến tại mục 1)

Ta có: \(AE+AF=AB+BE+AC+CF\) = \(AB+BG+AC+GC\)

= \(AB+AC+(BG+CG)=AB+AC+BC\) = \(a+b+c\)

Vì \(AE=AF\) => \(2AE=2AF\) = \(a+b+c\)  => \(AE=AF\) = \(\dfrac{a+b+c}{2}\)

b, Theo hình vẽ: \(BE=AE-AB\) = \(\dfrac{a+b+c}{2}\) - c = \(\dfrac{a+b+c}{2}\) - \(\dfrac{2c}{2}\) = \(\dfrac{a+b+c-2c}{2}\) = \(\dfrac{a+b-c}{2}\)

Vậy \(BE\) = \(\dfrac{a+b-c}{2}\)

c, Theo hình vẽ: \(CF=AF-AC\) = \(\dfrac{a+b+c}{2}\) - b = \(\dfrac{a+b+c}{2}\) - \(\dfrac{2b}{2}\) = \(\dfrac{a+b+c-2b}{2}\) = \(\dfrac{a-b+c}{2}\)

Vậy \(CF\) = \(\dfrac{a-b+c}{2}\)

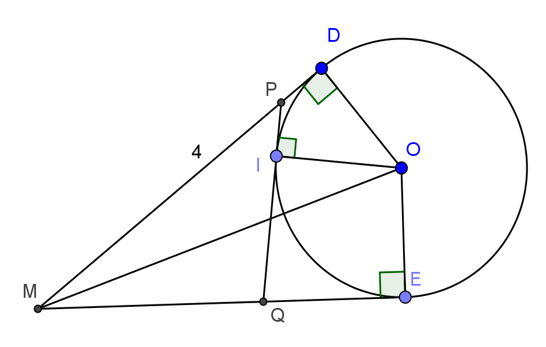
Bài 5: Cho một đường tròn tâm O với bán kính R và một đường thẳng d bất kỳ nằm bên ngoài đường tròn (giữa đường thẳng d và đường tròn tâm O bán kính R là không có điểm chung). Trên đường thẳng d lấy một điểm M tùy ý, xuất phát từ điểm M kẻ hai tiếp tuyến \(MA, MB\) đến đường tròn tâm O (\(A\), \(B\) là hai tiếp điểm). Từ tâm đường tròn O, kẻ \(OH\) đến đường thẳng d sao cho góc được tạo bởi \(OH\) và đường thẳng d bằng \(90^0\). Dây cung \(AB\) giao với đường thẳng \(OH\) tại điểm I, giao với đường thẳng \(OM\) tại điểm K. Hãy:

a, Sáng tỏ nhận định: \(OI.OH=OK.OM\)

b, Khi M di chuyển trên đường thẳng d thì K chuyển động trên đường thẳng nào?

Hướng dẫn giải bài tập:

a, Đường tròn tâm O \(MA\) và \(MB\) là hai tiếp tuyến với hai tiếp điểm \(A\) và \(B\) hai tiếp điểm

=> \(MA=MB\) (theo tính chất của hai tiếp tuyến tại mục 1)

Mà \(OA=OB=R\) (vì A, B là hai tiếp điểm) nên \(AB\) nhận \(OM\) là đường trung trực

=> \(OM\perp AB\)=> \(\widehat{OKI}=90^0\)

Xét trong phạm vi hai tam giác là \(OKI\) và \(OHM\), ta có:

\(\widehat{OKI}=\widehat{OHM}=90^0\)

\(\widehat{O}\) chung

=> \(\Delta OKI=\Delta OHM\) (theo trường hợp góc - góc)

=> \(OK.OM=OI.OH\) (điều phải chứng minh)

b, \(\Delta AMO\) có \(\widehat{A}=90^0\) và đường cao \(AK\), ta có:

\(OK.OM=OA^2\) => \(OI.OH\) = \(OK.OM\) = \(OA^2\) = \(R^2\) (vì A là tiếp điểm của đường tròn tâm O)

Vì tâm O của đường tròn, đường thẳng d và \(OH\) là cố định 

\(OI.OH=R^2\) không thay đổi và đường thẳng \(OH\) chứa điểm I nên I cố định

Theo ý a, \(\widehat{OKI}=90^0\) => K thuộc một đường tròn với \(OI\) là đường kính(góc chắn nửa đường tròn) mà OI không đổi nên khi M trong trạng thái di chuyển trên đường thẳng d thì K sẽ trong trạng thái dịch chuyển trên một đường tròn có đường kính OI không đổi

Tham khảo thêm >>> Giải bài tính chất của hai tiếp tuyến cắt nhau (sách giáo khoa)

Cunghocvui đã gửi đến các bạn bài lý thuyết các tính chất của hai tiếp tuyến cắt nhau và giải bài tính chất của hai tiếp tuyến cắt nhau thông qua bài giảng tính chất của hai tiếp tuyến cắt nhau. Nếu có đóng góp hay thắc mắc gì về bài tính chất của hai tiếp tuyến cắt nhau luyện tập, hãy để lại comment dưới phần bình luận nhé!