Giải bài 26 trang 115 - Sách giáo khoa Toán 9 tập 1
Đề bài
Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm).
a) Chứng minh rằng OA vuông góc với BC.
b) Vẽ đường kính CD. Chứng minh rằng BD song song với AO.
c) Tính độ dài các cạnh của tam giác ABC; biết OB = 2cm, OA = 4cm.
Hướng dẫn giải
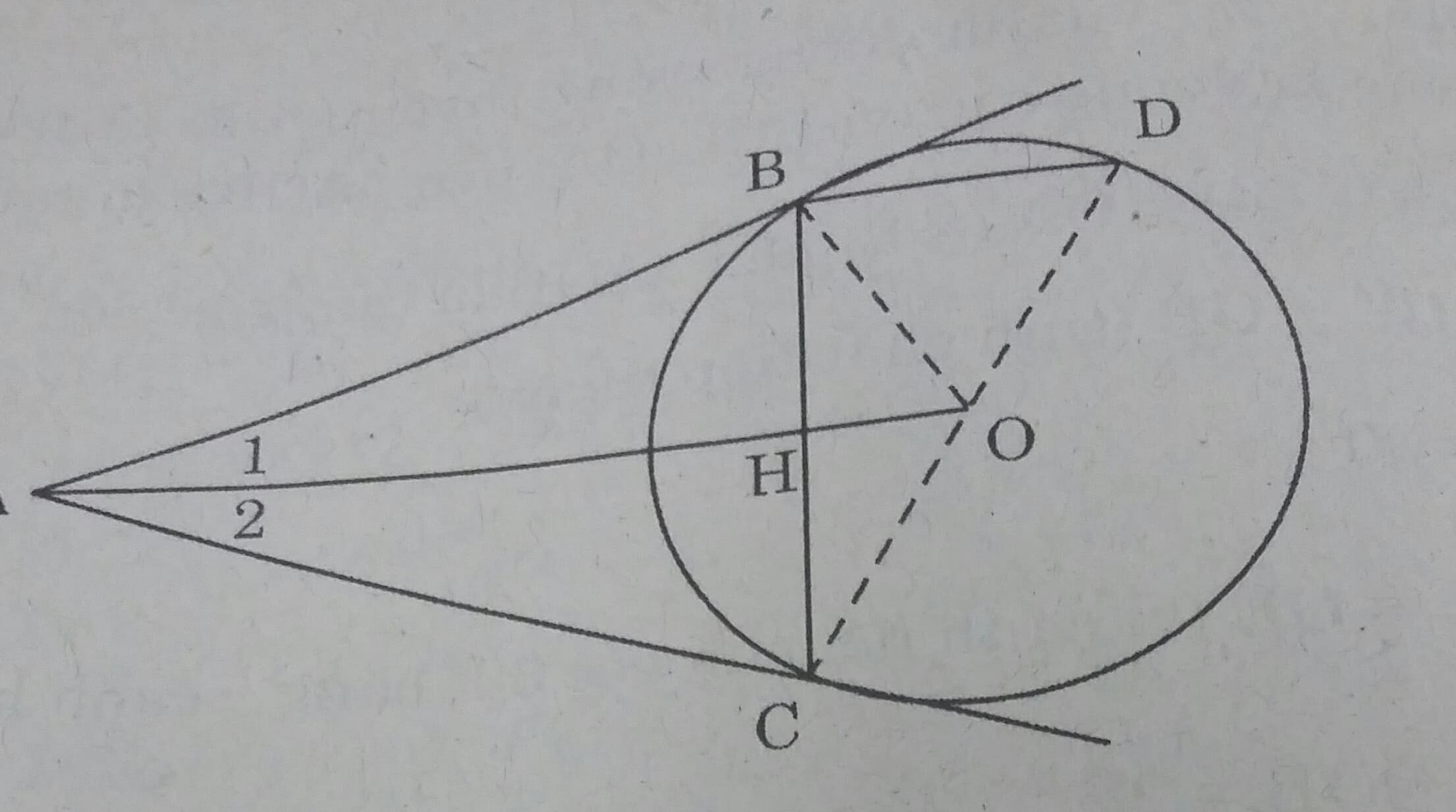
a) Ta có: AB,AC là các tiếp tuyến \( \Rightarrow AB=AC\)
Và \( \widehat{A_1}= \widehat{A_2}\) ( tính chất của hai tiếp tuyến cắt nhau) .
\( \Rightarrow \Delta ABC \) cân tại A và OA là phân giác.
\(\Rightarrow OA \perp BC\) ( tính chất tam giác cân)
b) \(\Delta BCD \) có OB =OC =OD ( bán kính)
\(\Rightarrow \Delta BCD \ vuông \ tại \ B \Rightarrow BD \perp BC \Rightarrow BD// OA\) ( cùng vuông góc với OA)
c) Tam giác vuông OBA có \(OB = \frac{1}{2}OA \Rightarrow \widehat{A_1}= 30^0 \Rightarrow \widehat{BAC}= 60^0 \Rightarrow \Delta ABC \) đều.
Áp dụng định lí Py-ta-go cho tam giác vuông OBA, ta được:
\(AB^2= OA^2-OB^2 = 4^2-2^2= 12 \Rightarrow AB = 2\sqrt{3}(cm)\)
Vậy AB= BC = CA= \(2\sqrt{3}\) m.

