Giải bài 39 trang 73 - Sách giáo khoa Toán 7 tập 2
Đề bài
Cho hình 39.
a) Chứng minh ΔABD = ΔACD
b) So sánh góc DBC và góc DCB.
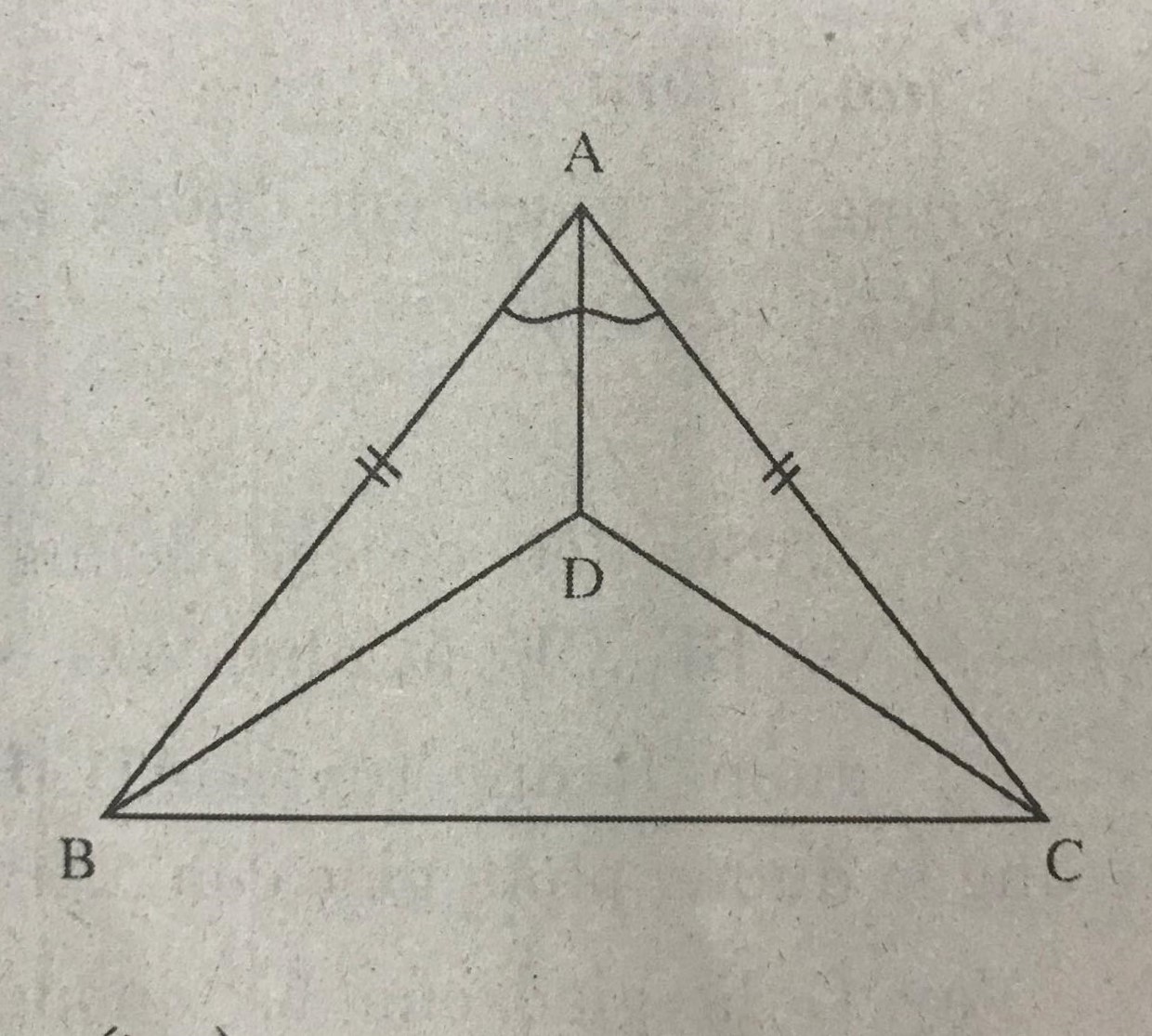
Hướng dẫn giải
a) \(\triangle\)ABD và \(\triangle\)ACD có :
AB = AC
\(\widehat{BAD}=\widehat{CAD}\)
AD là cạnh chung
Nên \(\triangle\)ABD = \(\triangle\)ACD (c.g.c)
b) \(\triangle\)ABD = \(\triangle\)ACD (câu a)
Suy ra : \(\widehat{ABD}=\widehat{ACD}\) (hai góc tương ứng)
Lại có AB = AC nên \(\triangle\)ABC cân ở A suy ra \(\widehat{ABC}=\widehat{ACB}\)
Do đó \(\widehat{DBC}=\widehat{DCB}\)

