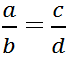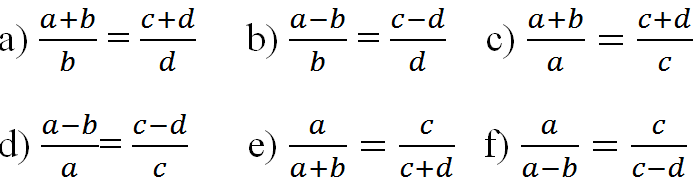Giải bài 102 trang 50 - Sách giáo khoa Toán 7 tập 1

Đề bài

 Từ tỉ lệ thức

(a, b, c, d ≠ 0, a ≠ ±b; c ≠ ±d) hãy suy ra các tỉ lệ thức sau

Hướng dẫn giải

a) Ta có : $\dfrac{a}{b}=\dfrac{c}{d} \Rightarrow \dfrac{a}{c} = \dfrac{b}{d}$

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có : $\dfrac{a}{c}=\dfrac{b}{d} = \dfrac{a+b}{c+d}$

Từ $\dfrac{b}{d} = \dfrac{a+b}{c+d}$$\Rightarrow \dfrac{a+b}{b}=\dfrac{c+d}{d}$

b) Ta có : $\dfrac{a}{b}=\dfrac{c}{d} \Rightarrow \dfrac{a}{c} = \dfrac{b}{d}$

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có : $\dfrac{a}{c}=\dfrac{b}{d} = \dfrac{a-b}{c-d}$

Từ $\dfrac{b}{d} = \dfrac{a-b}{c-d}$$\Rightarrow \dfrac{a-b}{b}=\dfrac{c-d}{d}$

c) Ta có : $\dfrac{a}{b}=\dfrac{c}{d} \Rightarrow \dfrac{a}{c} = \dfrac{b}{d}$

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có : $\dfrac{a}{c}=\dfrac{b}{d} = \dfrac{a+b}{c+d}$

Từ $\dfrac{a}{c} = \dfrac{a+b}{c+d}$$\Rightarrow \dfrac{a+b}{a}=\dfrac{c+d}{c}$

d) Ta có : $\dfrac{a}{b}=\dfrac{c}{d} \Rightarrow \dfrac{a}{c} = \dfrac{b}{d}$

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có : $\dfrac{a}{c}=\dfrac{b}{d} = \dfrac{a-b}{c-d}$

Từ $\dfrac{a}{c} = \dfrac{a-b}{c-d}$$\Rightarrow \dfrac{a-b}{a}=\dfrac{c-d}{c}$

e)  Ta có : $\dfrac{a}{b}=\dfrac{c}{d} \Rightarrow \dfrac{a}{c} = \dfrac{b}{d}$

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có : $\dfrac{a}{c}=\dfrac{b}{d} = \dfrac{a+b}{c+d}$

Từ $\dfrac{a}{c} = \dfrac{a+b}{c+d}$$\Rightarrow \dfrac{a}{a+b}=\dfrac{c}{c+d}$

f)  Ta có : $\dfrac{a}{b}=\dfrac{c}{d} \Rightarrow \dfrac{a}{c} = \dfrac{b}{d}$

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có : $\dfrac{a}{c}=\dfrac{b}{d} = \dfrac{a-b}{c-d}$

Từ $\dfrac{a}{c} = \dfrac{a-b}{c-d}$$\Rightarrow \dfrac{a}{a-b}=\dfrac{c}{c-d}$