Đề kiểm 15 phút - Đề số 6 - Bài 7 - Chương 3 - Hình học 9

Đề bài

Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm A và B. Gọi M là điểm tùy ý trên đường thẳng AB, nằm ngoài đoạn AB. Vẽ qua M hai cát tuyến MCD và MC’D’ với (O) và (O’). Chứng minh tứ giác CDD’C’ nội tiếp.

Hướng dẫn giải

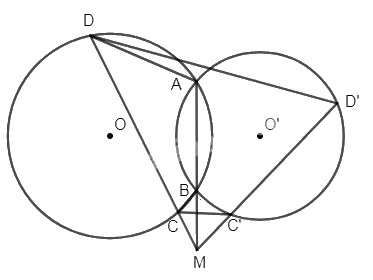
Ta có tứ giác ABCD nội tiếp trong đường tròn (O) nên \(\widehat {CDA} = \widehat {CBM}\) ( cùng bù với \(\widehat {ABC}\)).

Do đó \(∆MBC\) đồng dạng \(∆MDA \) (g.g)

\( \Rightarrow \dfrac{{MA}}{{MC}} =\dfrac {{MD} }{ {MB}}\)

\( \Rightarrow  MA.MB = MC.MD\)

Chứng minh tương tự :

\(MA.MB = MC’.MD’\)

\( \Rightarrow  MC.MD = MC’.MD’\)

Do đó \(∆MCC’\) đồng dạng \(∆MD’D\) (g.g)   

\( \Rightarrow \widehat {MCC'} = \widehat {MD'D}\)

Vậy tứ giác CDD’C’ nội tiếp.