Bài 31 trang 59 SGK Toán 9 tập 1

Đề bài

a) Vẽ đồ thị của hàm số :

\(y = x + 1;\,\,\,y = \dfrac{1}{\sqrt 3 }x + \sqrt 3 ;\,\,\,y = \sqrt 3 x - \sqrt 3\)

b) Gọi  \(\alpha ,\,\,\beta ,\,\,\,\gamma \)  lần lượt là các góc tạo bởi các đường thẳng trên và trục Ox.

Chứng minh rằng \(tg\alpha  = 1,\,\,\,tg\beta  = \dfrac{1}{\sqrt 3 };\,\,\,tg\gamma  = \sqrt 3\)

Tính số đo các góc α, β, ɣ.

Hướng dẫn giải

a) Cách vẽ đồ thị hàm số \(y=ax+b,\ (a \ne 0)\): Đồ thị hàm số \(y=ax+b \, \, (a\neq 0)\) là đường thẳng:

+) Cắt trục hoành tại điểm \(A(-\dfrac{b}{a}; \, 0).\) 

+) Cắt trục tung tại điểm \(B(0;b).\)

Xác định tọa độ hai điểm \(A\) và \(B\) sau đó kẻ đường thẳng đi qua hai điểm đó ta được đồ thị hàm số  \(y=ax+b \, \, (a\neq 0).\)

b) Góc tạo bởi đường thẳng \(y=a x+b \, \ (a \neq 0)\) là góc \(\alpha \) ta có: \(tan \alpha = a.\)

+) Với \(a<0\), góc \(\alpha\) là góc tù.

+) Với \(a>0\), góc \(\alpha\) là góc nhọn.

Hoặc sử dụng công thức lượng giác trong tam giác vuông:

      \(\Delta{ABC}\) vuông tại \(A\) khi đó: \(tan B = \dfrac{AC}{AB} \)

Lời giải chi tiết

a) 

+ \(y = x + 1\)

   Cho \(x=0 \Rightarrow y=0+1=1 \Rightarrow A(0; 1)\)

   Cho \(x=-1 \Rightarrow y=-1+1=0 \Rightarrow B(-1; 0)\)

Đồ thị hàm số \(y = x + 1\) là đường thẳng đi qua hai điểm \(A(0; 1)\) và \(B(-1; 0)\)

+ \(y = \dfrac{1}{\sqrt 3 }x + \sqrt 3\)

   Cho \(x=-3 \Rightarrow y = \dfrac{1}{\sqrt 3 }.(-3) + \sqrt 3=0  \Rightarrow D(-3; 0)\)

   Cho \(x=0 \Rightarrow y = \dfrac{1}{\sqrt 3 }.0 + \sqrt 3 =\sqrt 3 \Rightarrow C(0; \sqrt 3)\)

Đồ thị hàm \(y = \dfrac{1}{\sqrt 3 }x + \sqrt 3\) là đường thẳng đi qua hai điểm \(D(-3; 0)\) và \(C(0; \sqrt 3)\)

+ \(y = \sqrt 3 x - \sqrt 3\)

   Cho \(x=0 \Rightarrow y = \sqrt 3 .0 - \sqrt 3=\sqrt 3 \Rightarrow E(0; \sqrt 3)\)

   Cho \(x=1 \Rightarrow y = \sqrt 3 .1 - \sqrt 3=0 \Rightarrow F(1; 0)\)

Đồ thị hàm số \(y = \sqrt 3 x - \sqrt 3\) là đường thẳng đi qua hai điểm \(E(0; \sqrt 3)\) và \(F(1; 0)\)

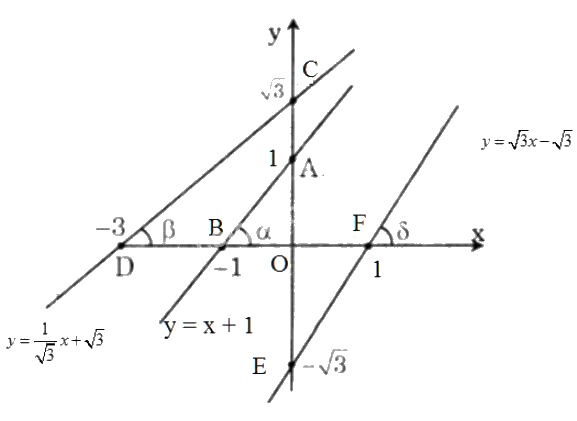
b)

Cách 1:

+ Đường thẳng \(y = x + 1\) có hệ số góc là \(1\)

Suy ra \(tan \alpha = 1 \Leftrightarrow \alpha = 45^o\)

+ Đường thẳng \(y = \dfrac{1}{\sqrt 3 }x + \sqrt 3\) có hệ số góc là \(\dfrac{1}{\sqrt 3 }\)

Suy ra \(tan \beta = \dfrac{1}{\sqrt 3 } \Leftrightarrow \beta = 30^o\)

+ Đường thẳng \(y = \sqrt 3 x - \sqrt 3\) có hệ số góc là \(\sqrt 3\)

Suy ra \(tan \gamma = \sqrt 3 \Leftrightarrow \alpha = 60^o\)

Cách 2:

+ Quan sát hình vẽ, dễ thấy:

\(OA=OB=OF=1\), \(OE=OC=\sqrt 3\),  \(OD = 3\).

+ Xét \(\Delta{OAB}\) vuông tại \(O\)

               \(\Rightarrow \tan \alpha =tan\ B =\dfrac{OA}{OB}=\dfrac{1}{1}=1\)

               \(\Rightarrow \alpha = 45^o\)  

Thực hiện bấm máy tính:

+ Xét \(\Delta{ODC}\) vuông tại \(O\)

                \(\Rightarrow \tan \beta =tan\ D =\dfrac{OC}{OD}=\dfrac{\sqrt 3}{3}\)

                \(\Rightarrow \beta = 30^o\)

+ Xét \(\Delta{OEF}\) vuông tại \(O\)

                \(\Rightarrow \tan \beta =tan \widehat{OFE} =\dfrac{OE}{OF}=\dfrac{\sqrt 3}{1}=\sqrt 3\)

                \(\Rightarrow \gamma  = 60^o\)

Lại có \(\widehat{OFE}\) và \(\gamma\) là hai góc đối đỉnh \(\Rightarrow \widehat{OFE}=\gamma\).

Vậy \(\gamma=60^o\).