Bài 11 trang 72 SGK Toán 9 tập 2

Đề bài

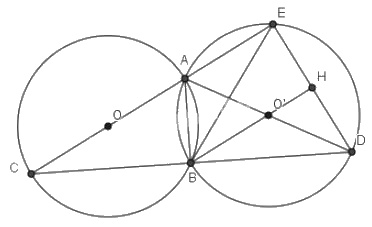
Cho hai đường tròn bằng nhau \((O)\) và \((O')\) cắt nhau tại hai điểm \(A\) và \(B\). Kẻ các đường kính \(AOC, AO'D\). Gọi \(E\) là giao điểm thứ hai của \(AC\) với đường tròn \((O')\).

a) So sánh các cung nhỏ \(\overparen{BC}, \overparen{BD}\).

b) Chứng minh rằng \(B\) là điểm chính giữa của cung \(\overparen{EBD}\) ( tức điểm \(B\) chia cung \(\overparen{EBD}\) thành hai cung bằng nhau: \(\overparen{BE}\) =  \(\overparen{BD}\) ).

Xem thêm

Hướng dẫn giải

Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:

a) Hai cung bằng nhau căng hai dây bằng nhau.

b) Hai dây bằng nhau căng hai cung bằng nhau.

Lời giải chi tiết

a) Nối \(C\) đến \(D\).

Ta có 2 đường tròn bằng nhau \(=> AC = AD\)

\(=> ∆ ACD\) cân tại \(A\)

Lại có \(\widehat{ABC} = 90^0\); do có \(OB = OC = OA = R\) ( tính chất trung tuyến ứng với cạnh huyền trong tam giác vuông )

Tương tự có \(\widehat{ABD} = 90^0\)

\(=> \widehat{ABC} + \widehat{ABD} = 180^0\)

\(=> C; B; D\) thẳng hàng và \(AB \bot CD\)

Nên trong tam giác cân ACD ta có đường cao AB cùng đồng thời là đường trung tuyến

\(=> BC = BD\)

=> \(\overparen{BC}\) = \(\overparen{BD}\)

b) Nối \(E\) đến \(D\); từ \(B\) hạ \(BH \bot ED\) Ta có góc \(\widehat{DEA} = 90^0\) ( chứng minh tương tự theo (a) )

nên \(CE \bot ED\)

\(=> BH // EC\)

Mà theo (a) ta có \(BE = BD\)

\(=> BH\) là đường trung bình tam giác \(CDE\)

\(=> HE = HD\) mà \(BH \bot ED => B\) là điểm chính giữa  \(\overparen{EBD}\)