Bài 10 trang 71 SGK Toán 9 tập 2

Đề bài

a) Vẽ đường tròn tâm \(O\) bán kinh \(R = 2\) cm. Nêu cách vẽ cung \(\overparen{AB}\) có số đo bằng \(60^0\). Hỏi dây \(AB\) dài bao nhiêu xentimet?

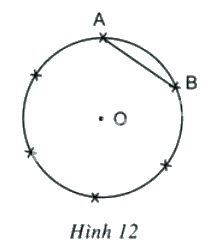
b) Làm thế nào để chia được đường tròn thành sáu cung bằng nhau như trên hình 12.

Hướng dẫn giải

a) Vẽ đường tròn \((O; R)\). Vẽ góc ở tâm có số đo  \(60^0\). Góc này chắn \(\overparen{AB}\) có số đo  \(60^0\) (hình a).

Tam giác \(AOB\) cân có \(\widehat{O}=60^0\) nên tam giác đều, suy ra \(AB = R\). 

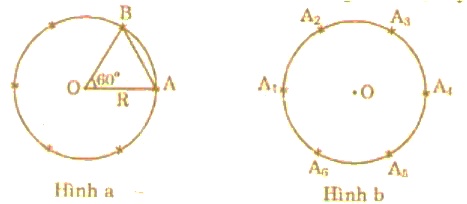
b) Theo câu a, ta có góc ở tâm bằng  \(sđ\overparen{AB}=60^0\). Số đo góc ở tâm vẽ được theo cách này là \(360^0:60^0= 6\). Suy ra được \(6\) cung tròn bằng nhau trên đường tròn.

Từ đó suy ra cách vẽ như sau:

Vẽ \(6\) dây cung bằng nhau và bằng bán kính \(R\):

\(\overparen{{A_1}{A_2}} = \overparen{{A_2}{A_3}} = \overparen{{A_3}{A_4}}= \overparen{{A_4}{A_5}} = \overparen{{A_5}{A_6}} = \overparen{{A_6}{A_1}}\)

\(= {\rm{ }}R\)

Từ đó suy ra \(6\) cung bằng nhau. (hình b)