Lý thuyết Liên hệ giữa cung và dây

Liên hệ giữa cung và dây là một trong những bài lý thuyết thuộc chương III Hình học Toán 9 nghiên cứu về Góc và đường tròn. Cunghocvui xin gửi tới các bạn bài lý thuyết liên hệ giữa cung và dây và cách làm bài tập liên hệ giữa cung và dây đầy đủ và chi tiết nhất. Mong bài viết toán 9 liên hệ giữa cung và dây sẽ giúp ích các bạn!

A. Một số lý thuyết cần nhớ về kiến thức mối liên hệ giữa cung và dây 

1. Định lý 1 về toán 9 liên hệ giữa cung và dây

Xét trong phạm vi là một đường tròn hoặc các đường tròn có độ lớn bằng nhau, ta có những tính chất sau:

- Hai cung có độ lớn bằng nhau thì căng được hai dây cung có độ lớn cũng bằng nhau.

Lấy ví dụ: \(\overbrace{AB}\) = \(\overbrace{CD}\) => \(AB\) = \(CD\)

- Tính chất 1 cũng đúng theo hướng ngược lại, có nghĩa là nếu hai dây cung có độ lớn bằng nhau thì căng được hai cung có độ lớn bằng nhau.

Lấy ví dụ: \(AB\) = \(CD\) => \(\overbrace{AB}\) = \(\overbrace{CD}\)

2. Định lý 2 về toán 9 liên hệ giữa cung và dây

Xét trong phạm vi là một đường tròn hoặc các đường tròn có độ lớn bằng nhau, ta có những tính chất sau:

- Cung nào có độ lớn lớn hơn thì căng một dây cung có độ lớn lớn hơn và ngược lại cung nào có độ lớn nhỏ hơn thì căng một dây cung có độ lớn nhỏ hơn.

Lấy ví dụ: \(\overbrace{AB}\) \(>\) \(\overbrace{CD}\) => \(AB\) \(>\) \(CD\)

- Tính chất 1 cũng đúng trong trường hợp ngược lại, có nghĩa là một dây cung có độ lớn lớn hơn sẽ căng một cung lớn hơn và ngược lại một dây cung có độ lớn nhỏ hơn thì căng một cung nhỏ hơn.

Lấy ví dụ: \(AB\) \(>\) \(CD\) => \(\overbrace{AB}\) \(>\) \(\overbrace{CD}\) 

3. Một số định lý bổ sung

- Định lý 1: Trong phạm vi của một đường trò nếu hai dây cung ở vị trí song song chắn giữa hai cung thì hai cung đó bằng nhau.

- Định lý 2: Trong phạm vi của một đường tròn:

+ Nếu một cung có điểm chính giữa nằm trên đường kính thì trung điểm của dây căng cung cũng nằm trên đường kính đó và ngược lại, nếu trung điểm của dây căng cung thuộc vào đường kính thì điểm chính giữa của dây căng cung cũng nằm trên đường kính đó.

+ Nếu một cung có điểm chính giữa nằm trên đường kính thì đường kính đó tạo với dây căng cung đó một góc bằng \(90^0\) và ngược lại, nếu đường kính đó tạo với dây căng cung đó một góc bằng \(90^0\) thì đường kính đi qua điểm chính giữa của cung đó.

B. Làm bài tập liên hệ giữa cung và dây

Bài 1: Cho \(AB\) là đường kính của một đường tròn với tâm là O và bán kính R. Điểm E trên đoạn \(OB\) chia đoạn thẳng này thành hai đoạn thẳng \(OE\) và \(EB\) bằng nhau. Xuất phát từ điểm E, kẻ một dây cung sao cho dây cung này tạo với \(OB\) một góc bằng \(90^0\) và giao với đường tròn lần lượt tại hai điểm là M và N. Xuất phát từ M, kẻ dây cung MP với một điều kiện là \(MP//AB\). Với cung nhỏ \(MP\), lấy I là điểm chính giữa và giao cắt của OI và PM được đặt tên là điểm K. Hãy:

a, Sáng tỏ đẳng thức: \(\overbrace{AP}\) = \(\overbrace{BN}\)

b, Sáng tỏ nhận định: Tứ giác OKME có dạng là một hình chữ nhật.

c, Sáng tỏ nhận định: \(KE//PN\)

Hướng dẫn giải bài tập bài 1:

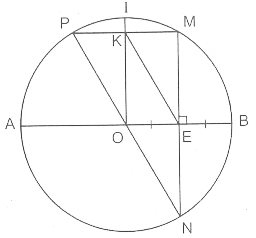
a, Theo giả thiết đề bài đưa ra, đường kính \(AB\) của một đường tròn với tâm là O và bán kính R tạo với dây cung \(MN\) một góc bằng \(90^0\) và giao điểm tại trung điểm E của dây cung \(MN\)

=> \(EM\) = \(EN\) và \(\overbrace{BM}\) = \(\overbrace{BN}\) (1)

Theo giả thiết, ta lại có: \(MP//AB\) => \(\overbrace{AP}\) = \(\overbrace{BM}\) (theo định lý cung bị chắn bởi hai dây cung song song)

Từ (1) và (2) => \(\overbrace{AP}\) = \(\overbrace{BN}\) (vì cùng bằng cung \(\overbrace{BM}\)) (điều phải chứng minh)

b, Theo giả thiết, vì bán kính \(OI\) cắt cung \(PM\) tại điểm chính giữa \(I\) 

=> \(KP\) = \(KM\) và \(OI\) \(\perp \) \(PM\) (3)

Vì \(MN\) đi qua \(AB\) và tạo với \(AB\) một góc bằng \(90^0\) mà \(MP//AB\)

=> \(MN\) \(\perp \) \(PM\) => \(\widehat{PMN}=90^0\)

Xét trong tứ giác OKME ta có \(\widehat{KME}\) = \(\widehat{OKM}\) = \(\widehat{MEO}\) \(=90^0\)

=> Vậy tứ giác OKME có dạng là một hình chữ nhật.

c, Sử dụng kết quả của ý a, ta có \(\overbrace{AP}\) = \(\overbrace{BN}\) => \(\widehat{AOP}\) = \(\widehat{BON}\) (liên hệ giữa cung và góc chắn cung)

Vì \(AB\) là đường kính của đường tròn tâm O bán kính R => Ba điểm A, O, B thẳng hàng

Mà \(\overbrace{AP}\) = \(\overbrace{BN}\) và \(\widehat{AOP}\) = \(\widehat{BON}\) => Ba điểm P, O, N cũng thẳng hàng

Xét trong tam giác \(PMN\) có \(KP\) = \(KM\) và \(EM\) = \(EN\)

=> \(KE\) là đường phân giác của tam giác \(PMN\) => \(KE//PN\) (điều phải chứng minh)

Cách 2 để chứng minh rằng \(KE//PN\) 

Tứ giác PKEO có dạng là một hình bình hành vì có hai yếu tố \(PK//OE\) và \(KP\) = \(OE\)

=> \(OP//KE\)

Tứ giác KENO có dạng là một hình bình hành vì có \(KE//ON\) và \(KE\) = \(ON\) = \(\dfrac{1}{2}\)R)

=> \(ON//KE\)

Vậy ba điểm P, O, N thẳng hàng.

Xét trong tam giác \(PMN\) có \(KP\) = \(KM\) và \(EM\) = \(EN\)

=> \(KE\) chia góc \(PMN\) thành hai góc bằng nhau => \(KE//PN\) (điều phải chứng minh)

Bài 2: Cho \(AB\) là đường kính của một đường tròn với tâm là O và bán kính R. Điểm C được lấy tùy ý. Điểm M và N lần lượt là điểm chính giữa của hai cung \(AC\) và \(CB\). Gọi I và K lần lượt là giao điểm cắt của OM với AC và ON với CB. Hỏi:

a, Tứ giác OICK mang dạng hình gì?

b, Giả sử OICK là hình vuông thì C nằm tại vị trí nào trên đường tròn?

Hướng dẫn giải bài tập bài 2: 

a, Theo giả thiết của đề bài: điểm M và N lần lượt là điểm chính giữa của hai cung \(AC\) và \(CB\) nên theo tính chất liên hệ dây và cung

=> \(ON\) \(\perp \) \(CB\) tại điểm K và \(OM\) \(\perp \) \(AC\) tại điểm I

=> \(\widehat{CIO}\) = \(\widehat{CKO}\) = \(90^0\)

Vì C thuộc (O,R) => \(\widehat{ACB}\) = \(90^0\) => \(\widehat{ICK}\) = \(90^0\) (vì I nằm trên \(AC\) và K nằm trên \(CB\))

Xét tứ giác OICK có \(\widehat{CIO}\) = \(\widehat{CKO}\) = \(\widehat{ICK}\) = \(90^0\) 

=> Tứ giác OICK có dạng là một hình chữ nhật.

b, Vì theo ý a, OICK là có dạng là một hình chữ nhật nên nếu muốn OICK là một hình vuông

=> \(IC\) = \(IK\) <=> \(2IC\) = \(2IK\) <=> \(CA\) = \(CB\)

Vì \(CA\) = \(CB\) nên \(\overbrace{AC}\) = \(\overbrace{AB}\) => Cung AB nhận C là điểm chính giữa

Vậy để OICK là một hình vuông thì vị trí của C trùng với điểm chính giữa của cung AB.

Bài 3: Trong phạm vi của một đường tròn tâm O với bán kính R, lấy một dây cung AB bất kỳ không đi qua tâm O. Trên dây cung AB bất kỳ đó lấy ba điểm C, D, E thỏa mãn điều kiện sau: \(AC\) = \(CD\) = \(DE\) = \(EB\). Gọi M, N, P lần lượt là các giao điểm của ba tia OC, OD, OE với đường tròn tâm O bán kính R. Hãy:

a, Sáng tỏ nhận định: \(\overbrace{AM}\) = \(\overbrace{PB}\) và \(\overbrace{MN}\) = \(\overbrace{NP}\)

b, Sáng tỏ nhận định: \(\overbrace{AM}\) < \(\overbrace{MN}\)

Hướng dẫn giải bài tập bài 3:

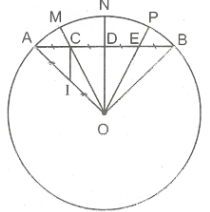
a, Chứng minh được rằng \(\widehat{AOM}\) = \(\widehat{BOP}\) => \(\overbrace{AM}\) = \(\overbrace{PB}\)

Mặt khác \(\overbrace{MN}\) =  \(\overbrace{AN}\) - \(\overbrace{AM}\), \(\overbrace{NP}\) =  \(\overbrace{BN}\) - \(\overbrace{PB}\)

Mà  \(\overbrace{AN}\) = \(\overbrace{NB}\) (tính chất của dây và cung) => \(\overbrace{MN}\) = \(\overbrace{NP}\)

b, Trên đoạn thẳng OA lấy I là trung điểm.

Trong tam giác \(AOD\) ta có: \(OA\) > \(OD\) (tính chất về độ dài ba cạnh của tam giác)

Tam giác \(AOD\) nhận IC là đường trung bình => \(IC\) = \(\dfrac{1}{2}\)\(OD\)

Mà \(OA\) > \(OD\) =>  \(OI\) > \(IC\) => \(\widehat{OCI}\) > \(\widehat{IOC}\) => \(\widehat{COD}\) > \(\widehat{AOC}\) 

=> \(\overbrace{MN}\) > \(\overbrace{AM}\) (điều phải chứng minh)

Bài 4: Với phạm vi là hai đường tròn đồng tâm tâm O bán kính R và bán kính R' với biểu thức liên hệ giữa R và R' là \(R=2R'\). Bên ngoài đường tròn tâm O bán kính R, lấy một điểm P bất kỳ. Xuất phát từ điểm P, vẽ một đường tròn tâm P bán kính PO. Đường tròn tâm P bán kính PO này cắt đường tròn tâm O bán kính R và đường tròn tâm O bán kính R' lần lượt tại hai điểm là E và F. Hai đoạn thẳng OC và OD cắt đường tròn tâm O bán kính R' tại hai điểm lần lượt là A và B. Hãy sáng tỏ các nhận định sau:

\(a, CD//EF\)

b, Đường tròn tâm O bán kính R' nhận lần lượt các đoạn thẳng PA và PB là các tiếp tuyến với A và B là các tiếp điểm.

Hướng dẫn giải bài tập bài 4:

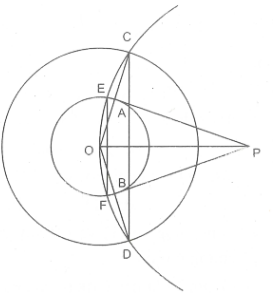
a, \(CD//EF\) vì cùng vuông góc với \(OP\)

b, Dây \(OC\) thuộc đường tròn tâm P bán kính PO nhận điểm A là trung điểm.

Tham khảo thêm >>> Giải bài tập liên hệ giữa cung và dây Toán 9

Cunghocvui đã đem lại cho các bạn bài viết lý thuyết về mối liên hệ giữa cung và dây và cách làm bài tập liên hệ giữa cung và dây qua bài viết toán 9 liên hệ giữa cung và dây đầy đủ nhất. Nếu có đóng góp hay thắc mắc gì về bài viết Toán 9 liên hệ giữa cung và dây, hãy để lại comment dưới phần bình luận nhé!