Giải bài 31 trang 79 - Sách giáo khoa Toán 9 tập 2

Đề bài

   

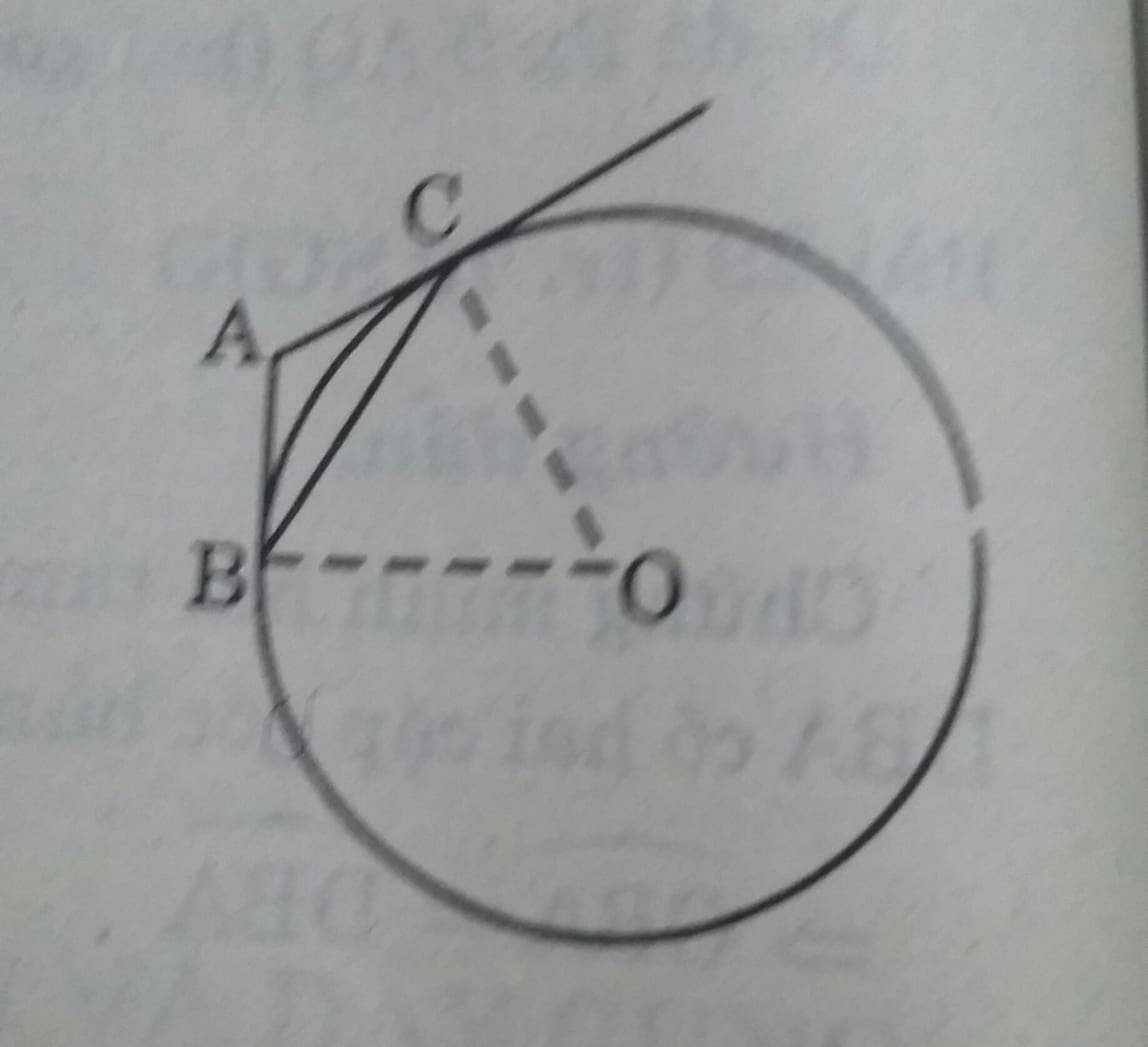
   Cho đường tròn (O; R) và dây cung BC = R . Hai tiếp tuyến của đường tròn (O) tại B, C cắt nhau ở A.

Hướng dẫn giải

   Vì BC =R nên \(\Delta BOC\) đều

 \( \Rightarrow \widehat{BOC}= 60^0 \Rightarrow \stackrel\frown{BC}=60^0\)

  Xét \(\Delta ABC \ có \widehat{B}= \widehat{C}= 60^0 : 2 = 30^0 \)( góc tạo bởi tia tiếp tuyến và dây cung)

  Suy ra \(\widehat{A}= 180^0 - (30^0+30^0)= 120^0\)