Giải bài 25 trang 112 - Sách giáo khoa Toán 9 tập 1

Đề bài

   Cho đường tròn tâm O có bán kính OA = R, dây BC vuông góc với OA tại trung điểm M của OA.

   a) Tứ giác OCAB là hình gì? Vì sao?

  b) Kẻ tiếp tuyến với đường tròn tại B, nó cắt đường thẳng OA tại E. Tính độ dài BE theo R.

Hướng dẫn giải

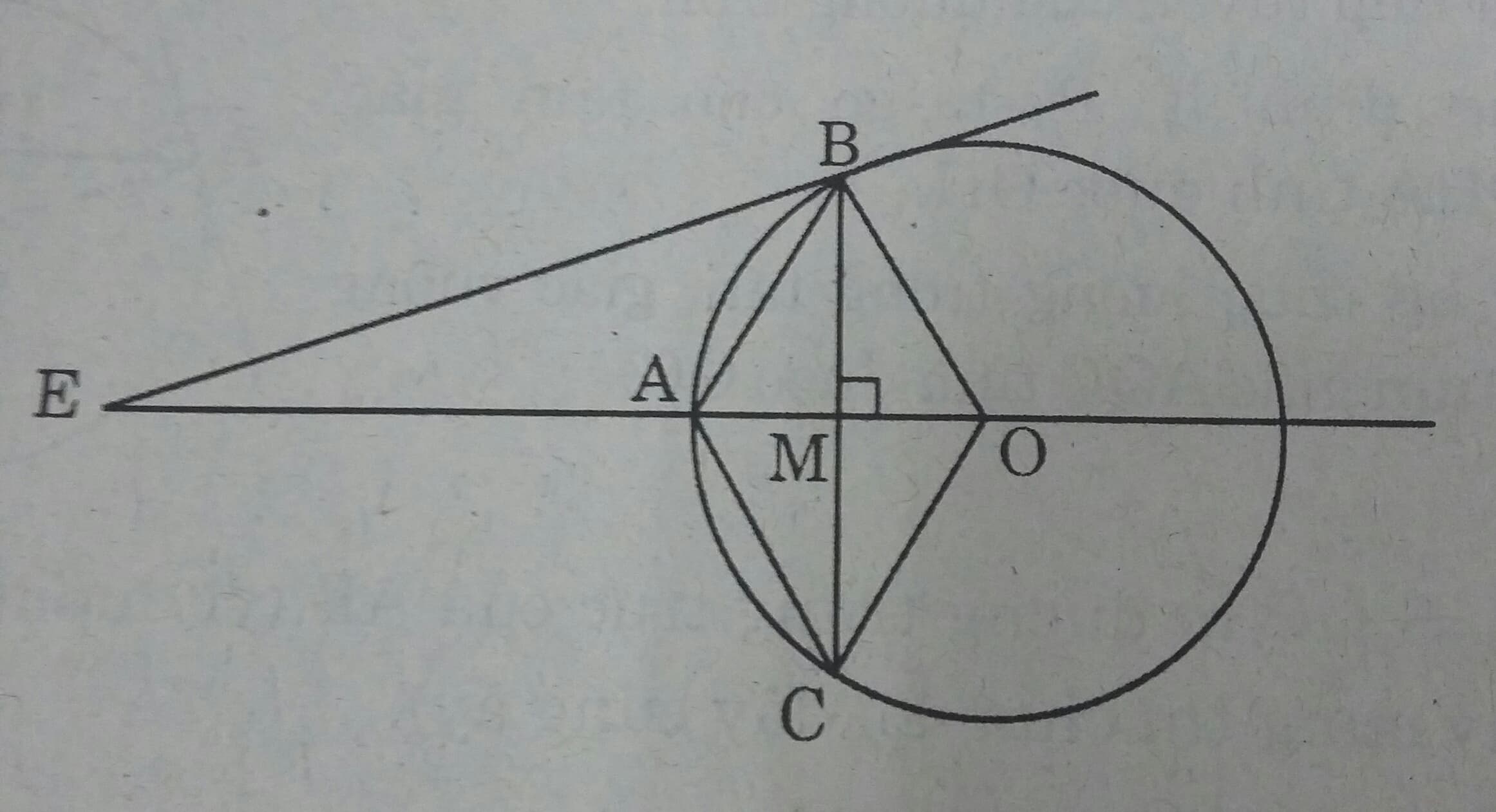
   a) MB= MC( Vì đường kính vuông góc với một dây thì chia đôi dây ấy)

      MA=MC (gt) 

   Suy ra: tứ giác ABOC là hình bình hành. 

Mặt khác: \( OA \perp BC\) (gt) nên hình bình hành ABOC là hình thoi.

b) \(\Delta AOB\) có BM vừa là đường trung tuyến ( Vì M là trung điểm của OA) vừa là đường cao ( Vì \(BC \perp OA) \ nên\ \Delta AOB\) cân tại B. 

 mặt khác OB=OA ( =R) nên \(\Delta AOB\)  là tam giác đều \( \Rightarrow \widehat{O}= 60^0\)

 Ta có: \(BE \perp OB \) ( tính chất tiếp tuyến) 

 \( \Rightarrow \widehat{E}=30^0 \Rightarrow OB = \frac{1}{2}OE\) ( Vì cạnh đối của góc \(30^0 \ bằng \ \frac{1}{2}\) cạnh huyền) 

  \( \Rightarrow OE= 2OB =2R\)

Áp dụng định lí Py-ta-go vào tam giác vuông OBE, ta được:

 \(BE^2=OE^2-OB^2=(2R)^2- R^2=3R^2 \Rightarrow BE= R \sqrt{3}\)