Giải bài 2 trang 7 - Sách giáo khoa Toán 9 tập 2

Đề bài

Với mỗi phương trình sau, tìm nghiệm tổng quát của phương trình và vẽ đường thẳng biểu diễn tập nghiệm của nó:

Hướng dẫn giải

Hướng dẫn:

Nghiệm tổng quát của phương trình ax + by = c.

Nếu \(a \neq 0\) thì tìm x theo y: \(x=\dfrac{c-by}{a}\) và công thức nghiệm tổng quát là: \(\left\{\begin{matrix}x=\dfrac{c-by}{a}\\ y \in R\end{matrix}\right.\)

Nếu \(b\neq 0\) thì tìm y theo x: \(y=\dfrac{c-ax}{b}\) và nghiệm tổng quát là: \(\left\{\begin{matrix}y=\dfrac{c-ax}{b}\\ x \in R\end{matrix}\right.\)

Vẽ đường thẳng biểu diễn tập nghiệm của phương trình ax + by = c.

Nếu \(b \neq 0\) thì vẽ đường thẳng \(y=-\dfrac{a}{b}x+\dfrac{c}{d}.\)

Nếu b = 0 thì vẽ đường thẳng \(x =\dfrac{c}{a}\) song song với trục tung.

Giải:

a) Ta có 3x - y = 2 \(\Leftrightarrow y=3x-2.\)

Nghiệm tổng quát của phương trình là:

\(\left\{\begin{matrix}y=3x-2\\ x \in R\end{matrix}\right.\)

Đường thẳng biểu diễn tập nghiệm của phương trình y = 3x - 2.

Cho x = 0 thì y = -2, ta xác định được điểm A(0; -2).

Cho y = 0 thì \(x=\dfrac{2}{3}\), ta xác định được điểm B(\(\dfrac{2}{3};0\)).

Vẽ đường thẳng AB.

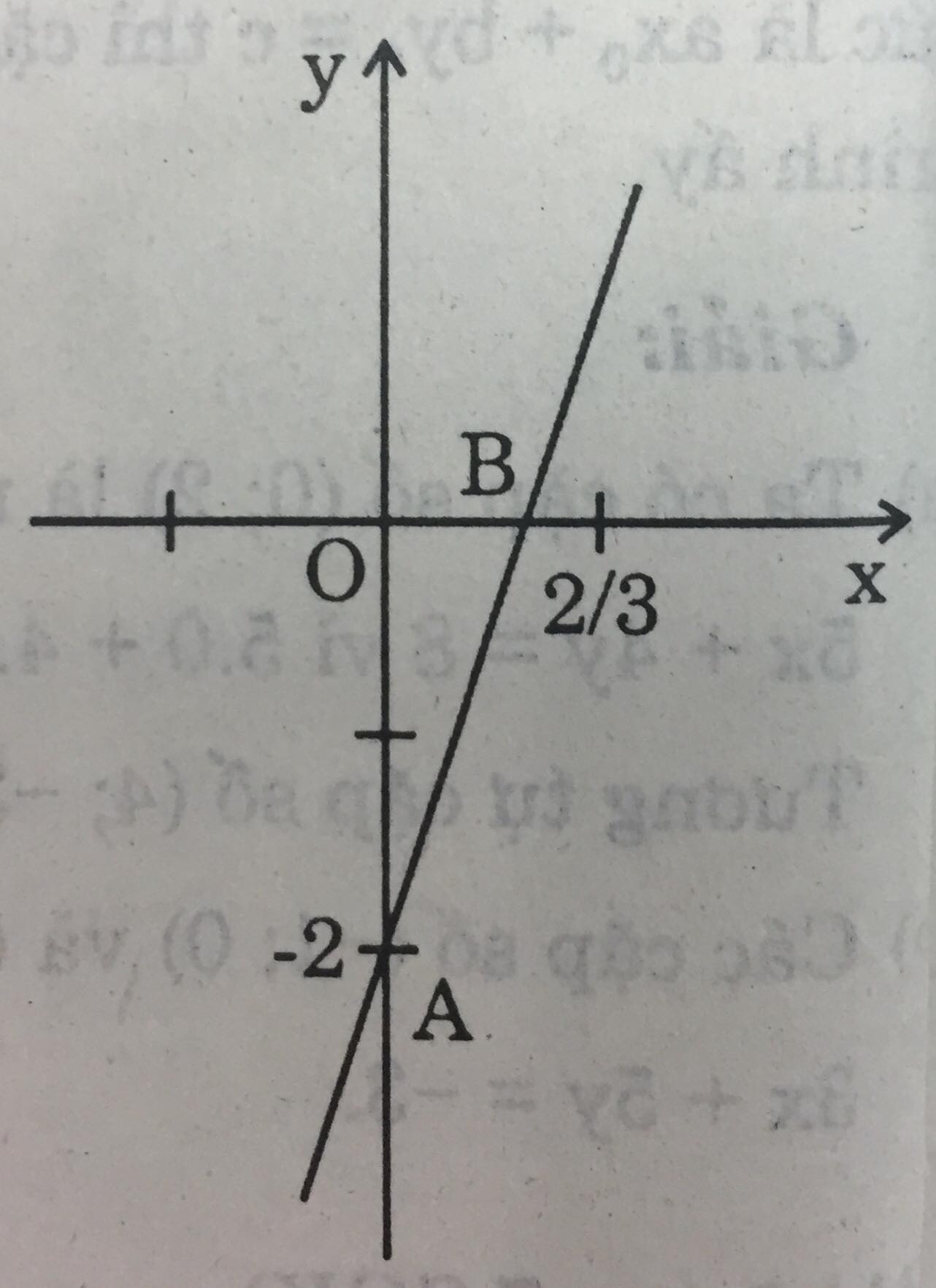
b) x + 5y = 3 \(\Leftrightarrow y =-\dfrac{1}{5}x+\dfrac{3}{5}\)

Nghiệm tổng quát của phương trình là: \(\left\{\begin{matrix}y=-\dfrac{1}{5}x+\dfrac{3}{5}\\ x \in R\end{matrix}\right.\)

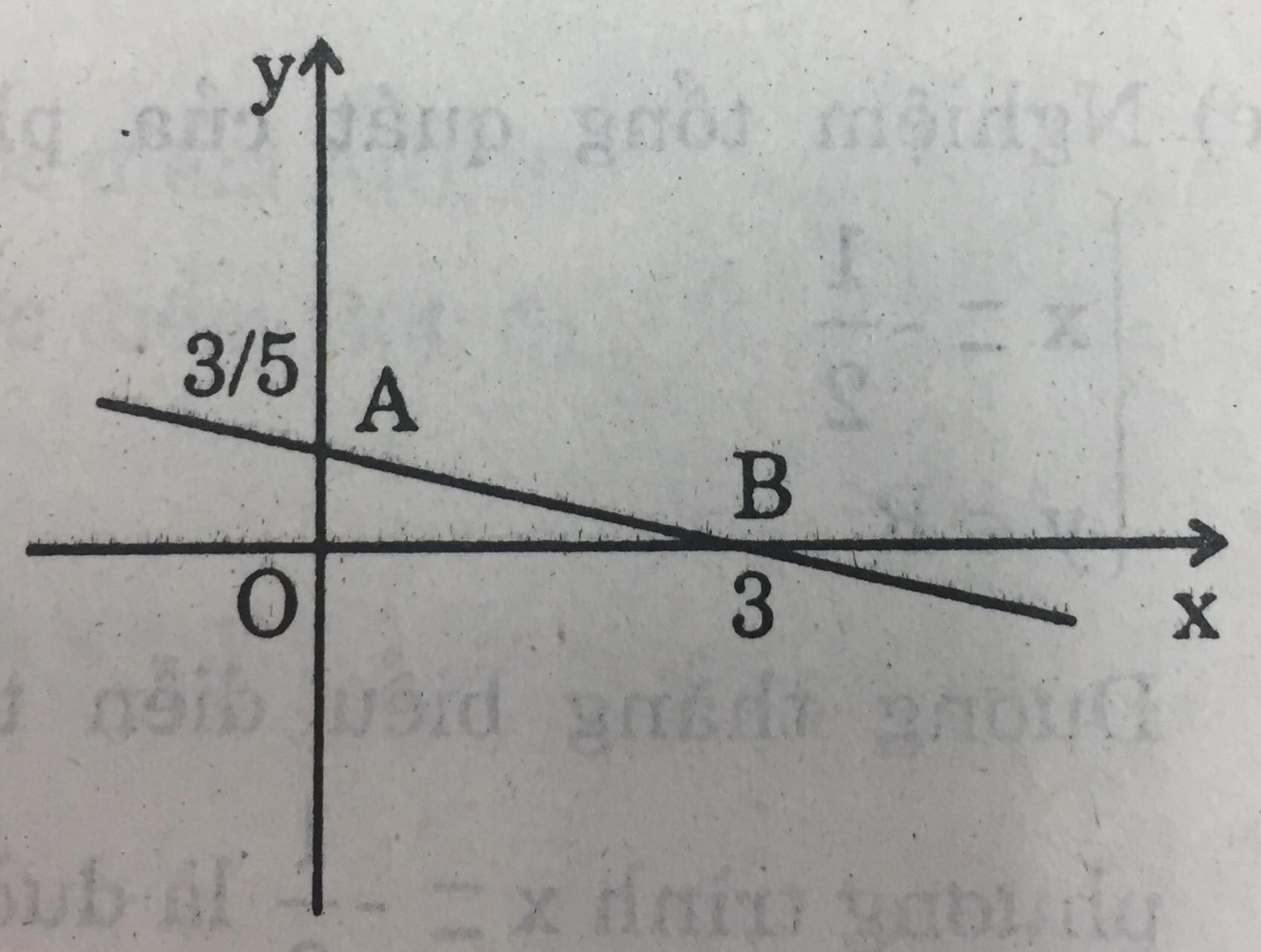
Đường biểu diễn tập nghiệm của phương trình: \(y=-\dfrac{1}{5}x+\dfrac{3}{5}\)

Cho x = 0 thì \(y=\dfrac{3}{5}\),  ta xác định được điểm \(A(0; \dfrac{3}{5})\).

Cho y = 0 thì x = 3, ta xác định được điểm B(3; 0).

Vẽ đường thẳng AB.

c) 4x - 3y = -1 \(\Leftrightarrow y =\dfrac{4}{3}x+\dfrac{1}{3}\)

Nghiệm tổng quát của phương trình là: \(\left\{\begin{matrix}y=\dfrac{4}{3}x+\dfrac{1}{3}\\ x \in R\end{matrix}\right.\)

Đường thẳng biểu diễn tập nghiệm của phương trình \(y=\dfrac{4}{3}x+\dfrac{1}{3}\).

Cho x = 0 thì \(y=\dfrac{1}{3}\), ta xác định được điểm A\((0; \dfrac{1}{3}).\)

Cho y = 0 thì \(x=-\dfrac{1}{4}\), ta xác định được điểm B\((-\dfrac{1}{4};0)\).

Vẽ đường thẳng AB.

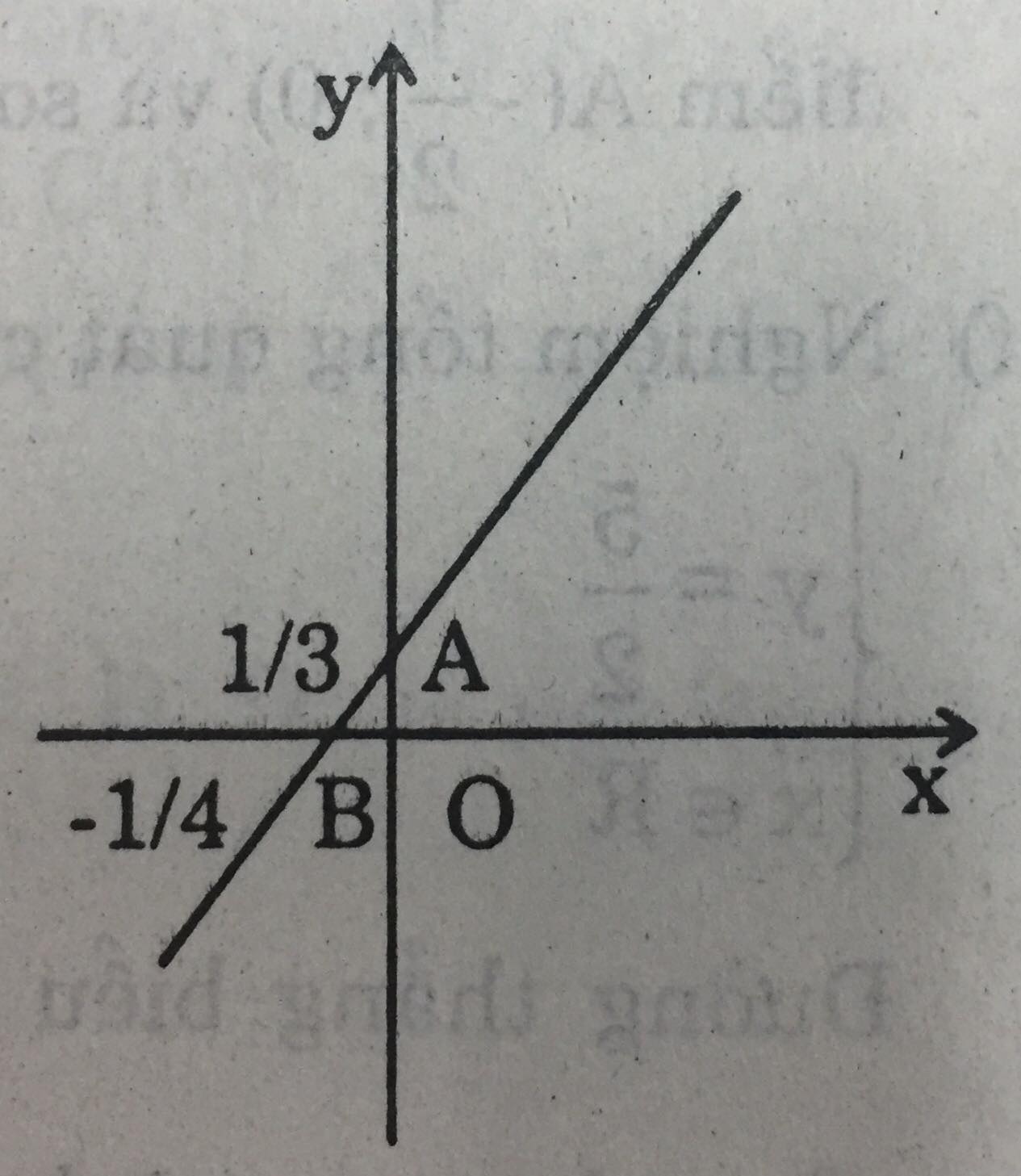
d) x + 5y = 0 \(\Leftrightarrow x =-5y\)

Nghiệm tổng quát của phương trình là: \(\left\{\begin{matrix}x=-5y\\ y \in R\end{matrix}\right.\)

Đường thẳng biểu diễn tập nghiệm của phương trình x = -5y.

Cho x = 0 thì y = 0, ta xác định được điểm O(0; 0).

Cho y = 1 thì x = -5, ta xác định được điểm A(-5; 1).

Vẽ đường thẳng OA.

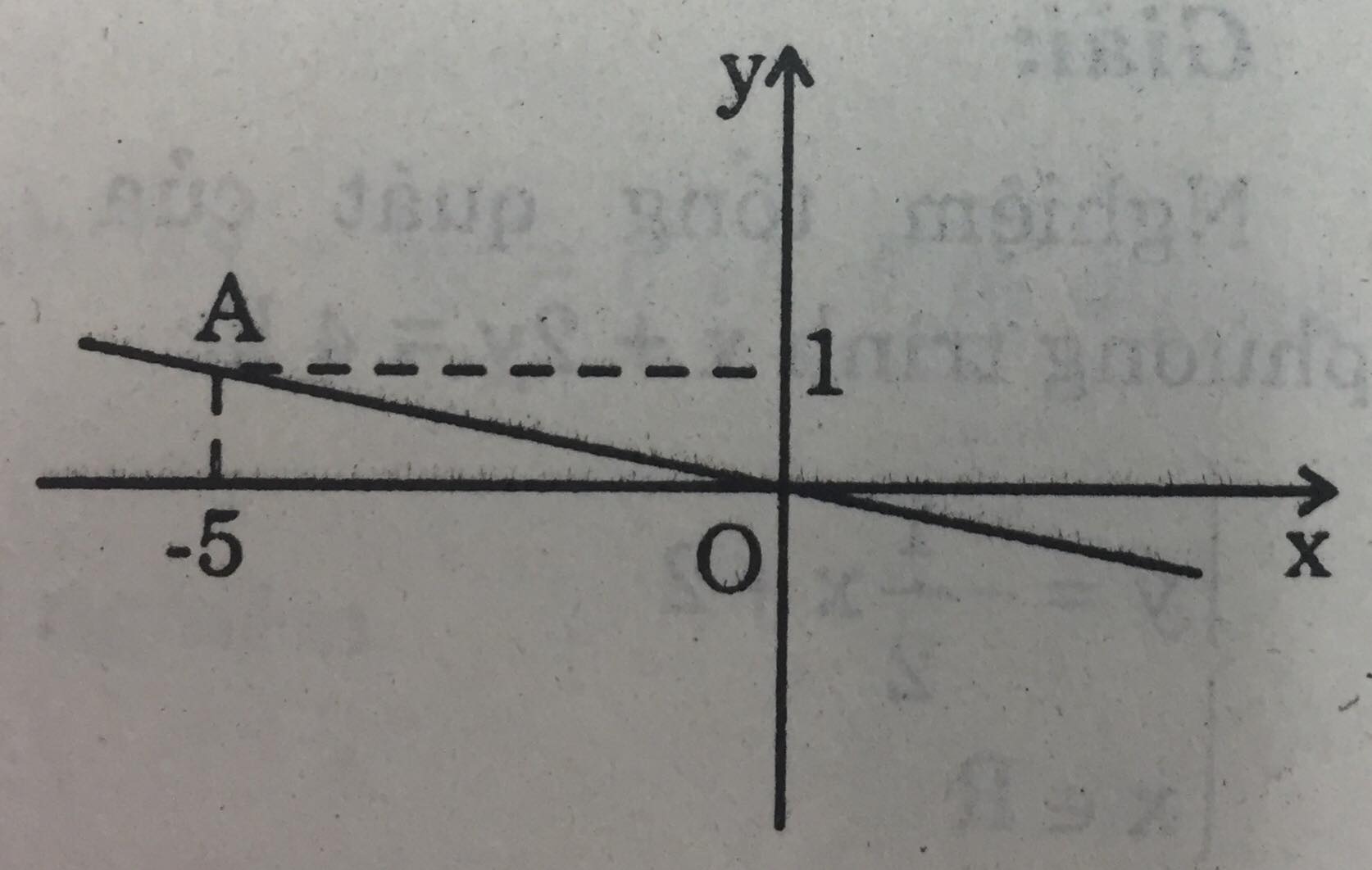
e) Nghiệm tổng quát của phương trình là: \(\left\{\begin{matrix}x=-\dfrac{1}{2}\\ y \in R\end{matrix}\right.\)

Đường thẳng biểu diễn tập nghiệm của phương trình \(x=-\dfrac{1}{2}\) là đường thẳng đi qua điểm A(\(-\dfrac{1}{2};0)\) và song song với trục Oy.

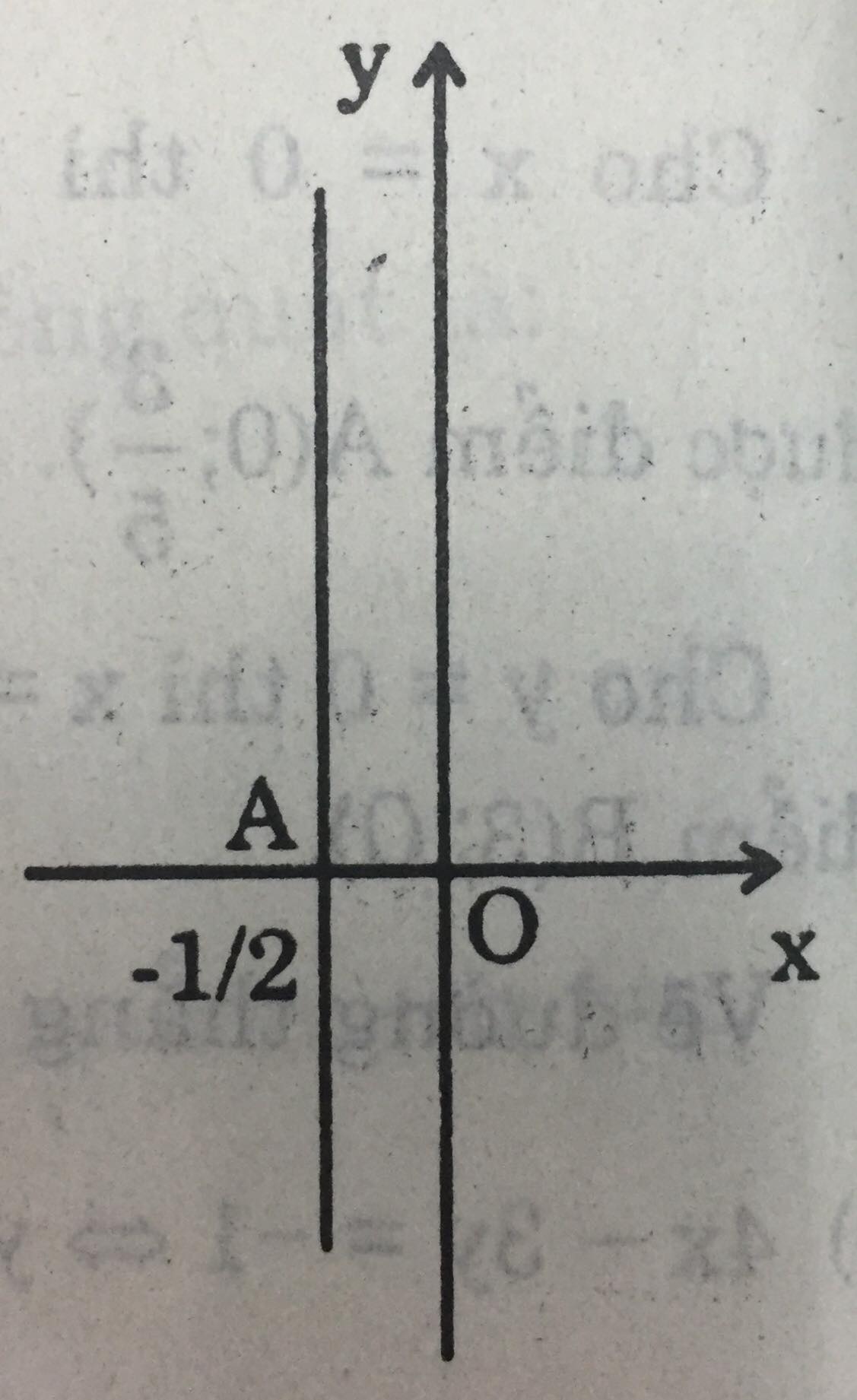
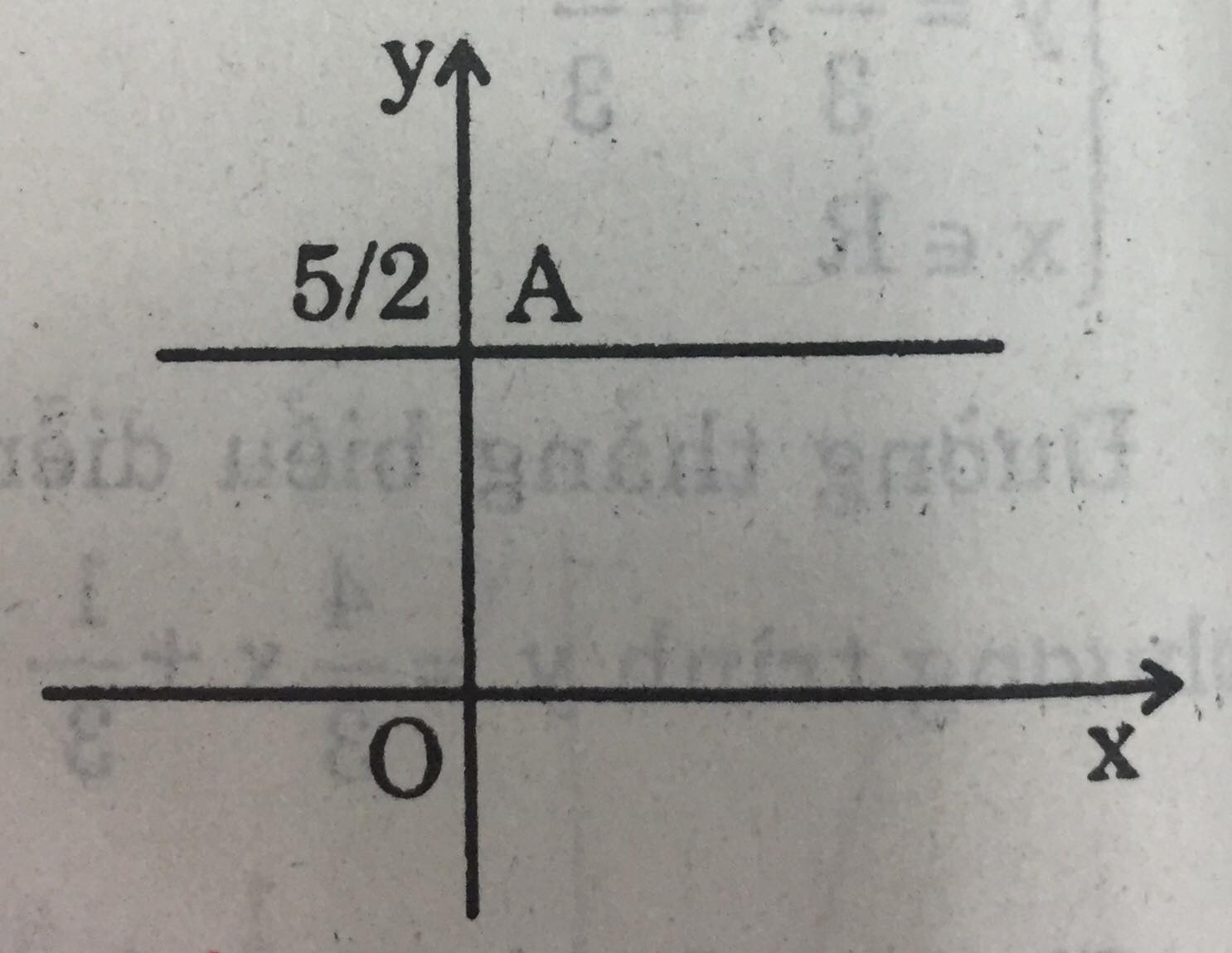
f) Nghiệm tổng quát của phương trình là: \(\left\{\begin{matrix}y=\dfrac{5}{2}\\ x \in R\end{matrix}\right.\)

Đường thẳng biểu diễn tập nghiệm của phương trình \(y=\dfrac{5}{2}\) là đường thẳng đi qua điểm \(A(0; \dfrac{5}{2})\) và song song với trục Ox.