Bài 52 trang 96 SGK Toán 8 tập 1
Đề bài
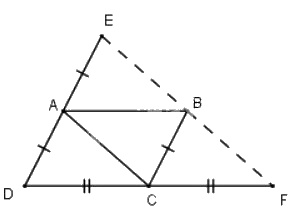
Cho hình bình hành \(ABCD\). Gọi \(E\) là điểm đối xứng với \(D\) qua điểm \(A\), gọi \(F\) là điểm đối xứng với \(D\) qua điểm \(C\). Chứng minh rằng điểm \(E\) đối xứng với điểm \(F\) qua điểm \(B\).
Hướng dẫn giải
Áp dụng: +) Tính chất hình bình hành.
+) Tính chất hai điểm đối xứng qua 1 điểm.
Lời giải chi tiết
Vì \(ABCD \) là hình bình hành (gt)
\( \Rightarrow A{\rm{D}}//BC, A{\rm{B}}//DC,\)\( A{\rm{D}}=BC, A{\rm{B}}=DC \) (tính chất hình bình hành)
Mà \(E \in A{\rm{D}}\) (gt) \( \Rightarrow AE//BC\)
Vì \(E\) là điểm đối xứng với \(D\) qua điểm \(A\)(gt)
\( \Rightarrow AE = A{\rm{D}}\) (tính chất hai điểm đối xứng qua 1 điểm)
\( \Rightarrow \) \(AE = BC\) (cùng bằng \(AD\))
\( \Rightarrow \) Tứ giác \(ACBE\) là hình bình hành (dấu hiệu nhận biết hình bình hành).
\( \Rightarrow \) \(BE // AC, BE = AC\) (1) (tính chất hình bình hành)
Ta có: \(AB//DC\left( {cmt} \right) \Rightarrow AB//CF\)
Vì \(F\) là điểm đối xứng với \(D\) qua điểm \(C\)(gt)
\( \Rightarrow CD = CF\) (tính chất hai điểm đối xứng qua 1 điểm)
\( \Rightarrow AB = CF\) (cùng bằng \(DC\))
\( \Rightarrow \) Tứ giác \(ACFB\) là hình bình hành (dấu hiệu nhận biết hình bình hành).
\( \Rightarrow \) \(BF // AC, BF = AC\) (2) (tính chất hình bình hành)
Từ (1) và (2) suy ra \(BE\) và \(BF\) cùng song song với \(AC\) và cùng đi qua điểm \(B\) nên theo tiên đề Ơclit \(BE\) trùng \(BF\) hay \(B, E, F\) thẳng hàng.
Lại có: \(BE\) = \(BF\) (cùng bằng \(AC\)) do đó \(B\) là trung điểm của \(EF\)
Vậy \(E\) đối xứng với \(F\) qua \(B\).

